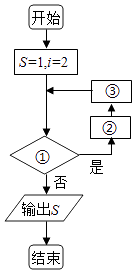
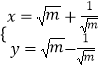题目内容
【题目】在平面直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),在以
为参数),在以 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 ![]() 是圆心为
是圆心为 ![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线 ![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设 ![]() 为曲线
为曲线 ![]() 上的点,
上的点, ![]() 为曲线
为曲线 ![]() 上的点,求
上的点,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:消去参数 ![]() 可得
可得 ![]() 的直角坐标方程为
的直角坐标方程为 ![]() .
.
曲线 ![]() 的圆心的直角坐标为
的圆心的直角坐标为 ![]() ,
,
∴ ![]() 的直角坐标方程为
的直角坐标方程为 ![]()
(2)解:设 ![]() ,
,
则 ![]()
![]() .
.
∵ ![]() ,∴
,∴ ![]() ,
, ![]() .
.
根据题意可得 ![]() ,
, ![]() ,
,
即 ![]() 的取值范围是
的取值范围是 ![]() .
.
【解析】(1)通过消去参数 φ即可得C1直角坐标方程,由题意可得C2的圆心直角坐标为(0,3),代入公式可得C2的直角坐标方程.
(2)通过设 点 M ( 2 c o s φ , s i n φ ),可得两点间距离公式可得| M C2|,由 1 ≤ sin φ ≤ 1可得| M C 2|的最大和最小值,从而可以得到 | M N | 的取值范围.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目