题目内容
【题目】现有一长为100码,宽为80码,球门宽为8码的矩形足球运动场地,如图所示,其中![]() 是足球场地边线所在的直线,球门
是足球场地边线所在的直线,球门![]() 处于所在直线的正中间位置,足球运动员(将其看做点
处于所在直线的正中间位置,足球运动员(将其看做点![]() )在运动场上观察球门的角
)在运动场上观察球门的角![]() 称为视角.
称为视角.
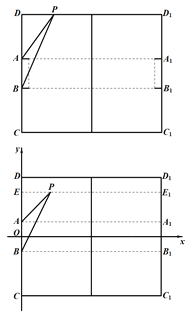
(1)当运动员带球沿着边线![]() 奔跑时,设
奔跑时,设![]() 到底线的距离为
到底线的距离为![]() 码,试求当
码,试求当![]() 为何值时
为何值时![]() 最大;
最大;
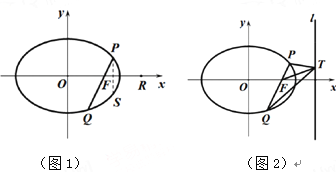
(2)理论研究和实践经验表明:张角![]() 越大,射门命中率就越大.现假定运动员在球场都是沿着垂直于底线的方向向底线运球,运动到视角最大的位置即为最佳射门点,以
越大,射门命中率就越大.现假定运动员在球场都是沿着垂直于底线的方向向底线运球,运动到视角最大的位置即为最佳射门点,以![]() 的中点为原点建立如图所示的直角坐标系,求在球场区域
的中点为原点建立如图所示的直角坐标系,求在球场区域![]() 内射门到球门
内射门到球门![]() 的最佳射门点的轨迹.
的最佳射门点的轨迹.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】
(1)要求得![]() 最大,只需
最大,只需![]() 最大,利用
最大,利用![]() ,将其展开后表示为关于x的函数,利用基本不等式求得最值.
,将其展开后表示为关于x的函数,利用基本不等式求得最值.
(2)设点![]() ,其中
,其中![]() ,
,![]() ,将
,将![]() 表示为关于x、y的函数,利用基本不等式求得取到最值时的条件,得到关于x,y的方程即为点的轨迹..
表示为关于x、y的函数,利用基本不等式求得取到最值时的条件,得到关于x,y的方程即为点的轨迹..
(1)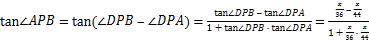
![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
又![]() 在
在![]() 上单调递增,∴当
上单调递增,∴当![]() 取得最大值时,
取得最大值时,![]() 最大,
最大,
∴![]() ,
,![]() 取得最大值
取得最大值![]() ;
;
(2)过点![]() 作
作![]() 于
于![]() ,设点
,设点![]() ,其中
,其中![]() ,
,![]() ,
,
∴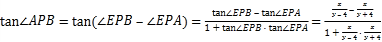
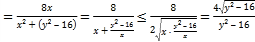 ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
此时轨迹方程为![]() ,
,
其表示焦点为![]() ,实轴长为8的等轴双曲线在
,实轴长为8的等轴双曲线在![]() 的一部分.
的一部分.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
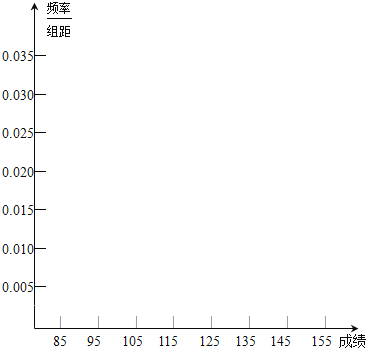
【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
| 12 |
|
|
| |
| 4 |
|
|
| |
合计 |
|
![]() 根据上面图表,求
根据上面图表,求![]() 处的数值
处的数值
![]() 在所给的坐标系中画出
在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
![]() 根据题中信息估计总体平均数,并估计总体落在
根据题中信息估计总体平均数,并估计总体落在![]() 中的概率.
中的概率.