题目内容
【题目】设椭圆
，点
为其右焦点，过点的直线与椭圆
相交于点
，
.
（1）当点在椭圆上运动时，求线段
的中点
的轨迹方程；
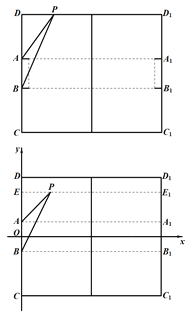
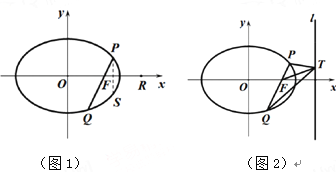
（2）如图1，点
的坐标为
，若点
是点关于
轴的对称点，求证：点，，共线；
（3）如图2，点
是直线
上的任意一点，设直线
，
，
的斜率分别为
，
，
，求证，，成等差数列.
【答案】（1）
； （2）见解析； （3）见解析.
【解析】
（1）设出中点
的坐标，利用点
的坐标得到
点的坐标，将点的坐标代入椭圆方程，化简得到点的轨迹方程.（2）当
斜率存在时，设出直线的方程，代入椭圆椭圆方程化简后写出韦达定理，计算
，由此证得点
，
，
共线. 当斜率不存在时，由椭圆对称性,易得结论成立.（3）设出
的坐标，利用（2）的结果化简
的表达式，化简得到结果为
，由此证得
，
，
成等差数列.
（1）
，设
，则
，在椭圆
上，所以所求轨迹方程为
.
（2）当斜率存在时，设其方程为：
，
，
将代入椭圆方程并化简得
其中
，
所以
，点，，共线，
而当斜率不存在时，由椭圆对称性，，重合，结论显然成立，综上点，，共线；
（3）设
， 
由（2）知
，
故，，成等差数列.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
