题目内容
【题目】对任意![]() ,函数
,函数![]() 满足:
满足:![]() ,
,![]() ,数列
,数列![]() 的前15项和为
的前15项和为![]() ,数列
,数列![]() 满足
满足![]() ,若数列
,若数列![]() 的前
的前![]() 项和的极限存在,则
项和的极限存在,则![]() ________.
________.
【答案】![]()
【解析】
由题意可得![]() ,0≤f(n)≤1,f(n+1)
,0≤f(n)≤1,f(n+1)![]() .展开代入可得
.展开代入可得![]() ,又
,又![]() ,化为
,化为![]() =
=![]() .再根据数列
.再根据数列![]() 的前15项和与
的前15项和与![]() ,解得
,解得![]() ,
,![]() .可得
.可得![]() ,
,![]() .解出f(2k﹣1),即可得出
.解出f(2k﹣1),即可得出![]() ,对n分奇偶分别求和并取极限,利用极限相等求得
,对n分奇偶分别求和并取极限,利用极限相等求得![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
展开为![]() ,
,![]() ,
,
即0≤f(n)≤1,![]() .
.
即![]() ,
,
∴![]() ,
,
化为![]() =
=![]() .
.
∴数列{![]() }是周期为2的数列.
}是周期为2的数列.
∵数列{![]() }的前15项和为
}的前15项和为![]() ,
,
∴![]() =7(
=7(![]() )+
)+![]() .
.
又![]() ,
,
解得![]() ,
,![]() .
.
∴![]() =
=![]() ,
,![]() =
=![]() .
.
由![]() 0,f(k+1)
0,f(k+1)![]() ,解得f(2k﹣1)
,解得f(2k﹣1)![]() .
.
![]() 0,f(n+1)
0,f(n+1)![]() ,解得f(2k)
,解得f(2k)![]() ,
,
又![]() ,
,
令数列![]() 的前n项和为
的前n项和为![]() ,则当n为奇数时,
,则当n为奇数时,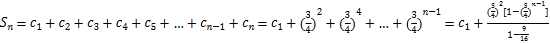 ,取极限得
,取极限得![]() ;
;
则当n为偶数时, ,取极限得
,取极限得![]() ;
;
若数列![]() 的前
的前![]() 项和的极限存在,则
项和的极限存在,则![]() ,
,![]() ,
,
故答案为![]() .
.

练习册系列答案
相关题目
【题目】已知函数f(x)=(x2﹣a)ex(a∈R).
(1)若函数f(x)有两个不同的极值点,求实数a的取值范围;
(2)当a=0时,若关于x的方程f(x)=m存在三个不同的实数根,求实数m的取值范围.
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|