题目内容
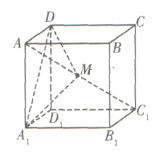
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),则下列结论正确的是__________
不重合),则下列结论正确的是__________
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
③![]() 的面积可能等于
的面积可能等于![]() ;
;
④若![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]()
【答案】①②③④
【解析】
根据正方体的结构特征,利用线面位置关系的判定定理和性质定理,以及三角形的面积公式和投影的定义,即可求解,得到答案.
①如图所示,当![]() 是
是![]() 中点时,可知
中点时,可知![]() 也是
也是![]() 中点且
中点且![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,同理可知
,同理可知![]() ,
,
且![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,故正确;
,故正确;

②如图所示,取![]() 靠近
靠近![]() 的一个三等分点记为
的一个三等分点记为![]() ,记
,记![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() 为
为![]() 靠近
靠近![]() 的一个三等分点,
的一个三等分点,
则![]() 为
为![]() 中点,又
中点,又![]() 为
为![]() 中点,所以
中点,所以![]() ,且
,且![]() ,
,![]() ,
,![]() ,所以平面
,所以平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,故正确;
,故正确;
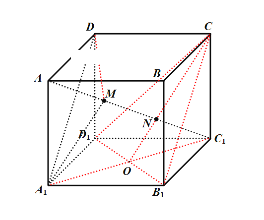
③如图所示,作![]() ,在
,在![]() 中根据等面积得:
中根据等面积得:![]() ,
,
根据对称性可知:![]() ,又
,又![]() ,所以
,所以![]() 是等腰三角形,
是等腰三角形,
则 ,故正确;
,故正确;

④如图所示,设![]() ,
,![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,
,![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,所以
,所以![]() ,
,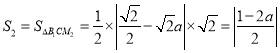 ,当
,当![]() 时,解得:
时,解得:![]() ,故正确.
,故正确.

故答案为 ①②③④


练习册系列答案
相关题目
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|