题目内容
(14分)若f(x)=2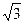 sin
sin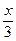 cos
cos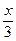 -2sin2
-2sin2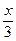 . (1)若x∈[0,π],求f(x)的值域; (2)在△ABC中,A、B、C所对边分别为a、b、c,若f(C)=1,且b2=ac,求sinA的值.
. (1)若x∈[0,π],求f(x)的值域; (2)在△ABC中,A、B、C所对边分别为a、b、c,若f(C)=1,且b2=ac,求sinA的值.
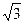 sin
sin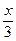 cos
cos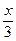 -2sin2
-2sin2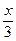 . (1)若x∈[0,π],求f(x)的值域; (2)在△ABC中,A、B、C所对边分别为a、b、c,若f(C)=1,且b2=ac,求sinA的值.
. (1)若x∈[0,π],求f(x)的值域; (2)在△ABC中,A、B、C所对边分别为a、b、c,若f(C)=1,且b2=ac,求sinA的值.(1)[0,1] (2)

(1)f(x)=2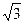 sin
sin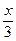 cos
cos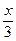 -2sin2
-2sin2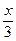
=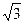 sin
sin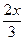 +cos
+cos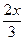 -1=2sin(
-1=2sin(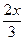 +
+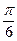 )-1,
)-1,
当x∈[0,π]时,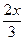 +
+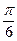 ∈[
∈[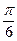 ,
,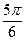 ],∴当x∈[0,π]时,f(x)∈[0,1];
],∴当x∈[0,π]时,f(x)∈[0,1];
(2)由(1)知f(x)=2sin(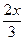 +
+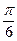 )-1,而f(C)=1,
)-1,而f(C)=1,
则可得2sin(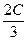 +
+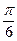 )-1=1,即sin(
)-1=1,即sin(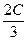 +
+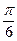 )=1,那么
)=1,那么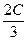 +
+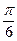 =
=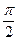 +2kπ,k∈Z,
+2kπ,k∈Z,
即C=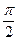 +3kπ,k∈Z,而C∈(0,π),则C=
+3kπ,k∈Z,而C∈(0,π),则C=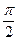
那么c2=a2+b2=a2+ac,即a2+ac-c2=0,由正弦定理可得sin2A+sinA-1=0,
解得sinA= (负值舍去).
(负值舍去).
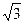 sin
sin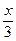 cos
cos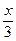 -2sin2
-2sin2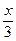
=
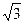 sin
sin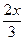 +cos
+cos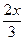 -1=2sin(
-1=2sin(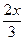 +
+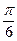 )-1,
)-1,当x∈[0,π]时,
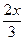 +
+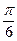 ∈[
∈[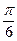 ,
,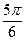 ],∴当x∈[0,π]时,f(x)∈[0,1];
],∴当x∈[0,π]时,f(x)∈[0,1];(2)由(1)知f(x)=2sin(
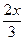 +
+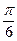 )-1,而f(C)=1,
)-1,而f(C)=1,则可得2sin(
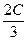 +
+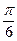 )-1=1,即sin(
)-1=1,即sin(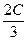 +
+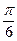 )=1,那么
)=1,那么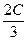 +
+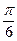 =
=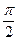 +2kπ,k∈Z,
+2kπ,k∈Z,即C=
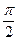 +3kπ,k∈Z,而C∈(0,π),则C=
+3kπ,k∈Z,而C∈(0,π),则C=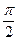
那么c2=a2+b2=a2+ac,即a2+ac-c2=0,由正弦定理可得sin2A+sinA-1=0,
解得sinA=
 (负值舍去).
(负值舍去).
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
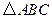 中,
中,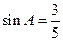 ,
,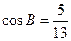 ,求
,求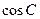 的值.
的值.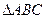 中,
中, 分别为三个内角A、B、C所对的边,设向量
分别为三个内角A、B、C所对的边,设向量
 ,若向量
,若向量 ,则角C的大小为 。
,则角C的大小为 。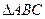 中,
中,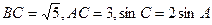
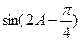 的值。
的值。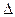 ABC中,
ABC中,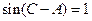 , sinB=
, sinB=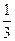 .
.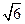 ,求
,求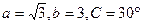 ,则A= 。
,则A= 。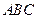 中,若
中,若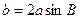 ,则
,则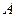 等于( )
等于( )