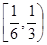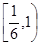题目内容
已知二次函数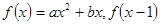 为偶函数,集合A=
为偶函数,集合A=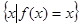 为单元素集合
为单元素集合
(I)求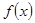 的解析式
的解析式
(II)设函数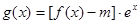 ,若函数
,若函数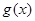 在
在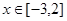 上单调,求实数
上单调,求实数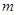 的取值范围.
的取值范围.
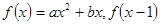 为偶函数,集合A=
为偶函数,集合A=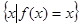 为单元素集合
为单元素集合(I)求
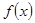 的解析式
的解析式(II)设函数
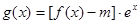 ,若函数
,若函数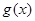 在
在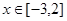 上单调,求实数
上单调,求实数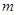 的取值范围.
的取值范围.(I)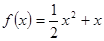
(II)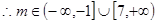
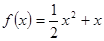
(II)
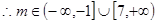
(I)因为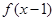 为偶函数,所以二次函数的对称轴为x=-1,又因为
为偶函数,所以二次函数的对称轴为x=-1,又因为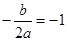 ,又因为f(x)=x只有一个根,所以
,又因为f(x)=x只有一个根,所以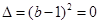 ,所以b=1,a=
,所以b=1,a=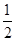 .
.
所以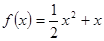 .
.
(II) 本小题要讨论g(x)是增函数还是减函数,
若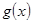 在
在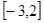 上单调递增,实质上
上单调递增,实质上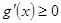 在
在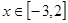 上恒成立,
上恒成立,
即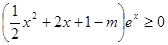 在
在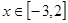 上恒成立,即
上恒成立,即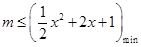 .
.
若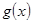 在
在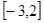 上单调递减,则
上单调递减,则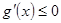 在
在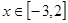 上恒成立,
上恒成立,
即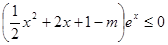 在
在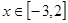 上恒成立,即
上恒成立,即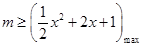 ,
,
最好求并集即可.
解:(I)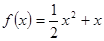
(II)若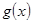 在
在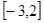 上单调递增,则
上单调递增,则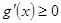 在
在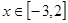 上恒成立,
上恒成立,
即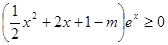 在
在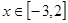 上恒成立,即
上恒成立,即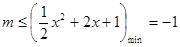
若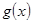 在
在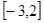 上单调递减,则
上单调递减,则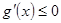 在
在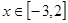 上恒成立,
上恒成立,
即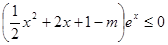 在
在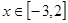 上恒成立,即
上恒成立,即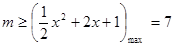
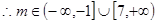
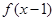 为偶函数,所以二次函数的对称轴为x=-1,又因为
为偶函数,所以二次函数的对称轴为x=-1,又因为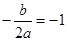 ,又因为f(x)=x只有一个根,所以
,又因为f(x)=x只有一个根,所以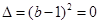 ,所以b=1,a=
,所以b=1,a=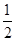 .
.所以
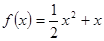 .
.(II) 本小题要讨论g(x)是增函数还是减函数,
若
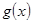 在
在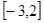 上单调递增,实质上
上单调递增,实质上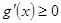 在
在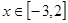 上恒成立,
上恒成立,即
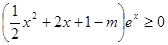 在
在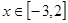 上恒成立,即
上恒成立,即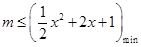 .
.若
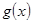 在
在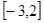 上单调递减,则
上单调递减,则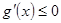 在
在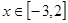 上恒成立,
上恒成立,即
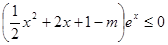 在
在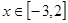 上恒成立,即
上恒成立,即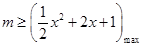 ,
,最好求并集即可.
解:(I)
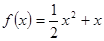
(II)若
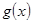 在
在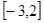 上单调递增,则
上单调递增,则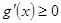 在
在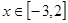 上恒成立,
上恒成立,即
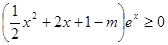 在
在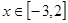 上恒成立,即
上恒成立,即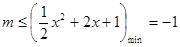
若
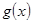 在
在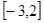 上单调递减,则
上单调递减,则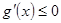 在
在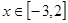 上恒成立,
上恒成立,即
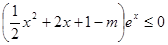 在
在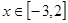 上恒成立,即
上恒成立,即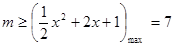

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
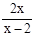 ,
, 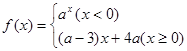 满足对任意
满足对任意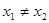 ,都有
,都有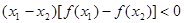 成立,则
成立,则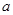 的取值范围为( )
的取值范围为( )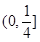
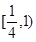
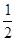 )=0,则不等式f(log4x)>0的解集是______________.
)=0,则不等式f(log4x)>0的解集是______________.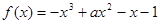 在
在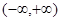 上是单调函数,则实数
上是单调函数,则实数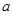 的取值范围是( )
的取值范围是( )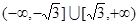
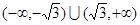
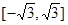
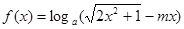 在R上为奇函数,
在R上为奇函数,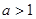 ,
,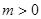 .
.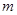 的值;
的值;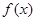 的单调性.(不需要证明)
的单调性.(不需要证明)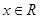 ,都有
,都有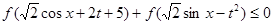 ;是否存在
;是否存在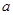 的值,使
的值,使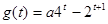 最小值为
最小值为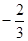 ;
;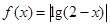 ,在其上为增函数的是( )
,在其上为增函数的是( )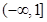
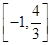
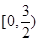
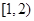
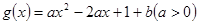 ,在区间
,在区间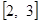 上有最大值4、最小值1,设函数
上有最大值4、最小值1,设函数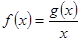 。
。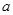 、
、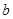 的值;
的值;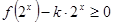 在
在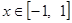 上恒成立,求
上恒成立,求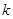 的取值范围。
的取值范围。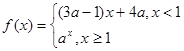 是
是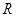 上减函数,则
上减函数,则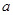 的取值范围是( )
的取值范围是( )