题目内容
已知函数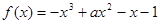 在
在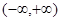 上是单调函数,则实数
上是单调函数,则实数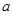 的取值范围是( )
的取值范围是( )
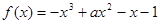 在
在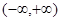 上是单调函数,则实数
上是单调函数,则实数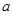 的取值范围是( )
的取值范围是( )A.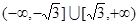 | B.(-∞,2) |
C.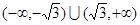 | D.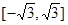 |
D
由f(x)=-x3+ax2-x-1,得到f′(x)=-3x2+2ax-1,
因为函数在(-∞,+∞)上是单调函数,
所以f′(x)=-3x2+2ax-1≤0在(-∞,+∞)恒成立,
则△=4a2-12≤0,解得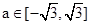 ,故选D
,故选D
因为函数在(-∞,+∞)上是单调函数,
所以f′(x)=-3x2+2ax-1≤0在(-∞,+∞)恒成立,
则△=4a2-12≤0,解得
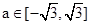 ,故选D
,故选D
练习册系列答案
相关题目
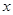 ,设
,设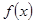 取
取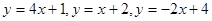 三个函数中的最小值,用分段函数写出
三个函数中的最小值,用分段函数写出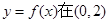 上是增函数,函数
上是增函数,函数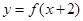 是偶函数,则下列结论正确的是( )
是偶函数,则下列结论正确的是( )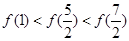
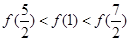
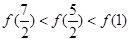
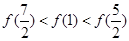
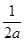 -
-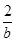 的上确界为( )
的上确界为( )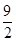
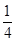
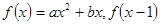 为偶函数,集合A=
为偶函数,集合A=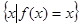 为单元素集合
为单元素集合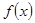 的解析式
的解析式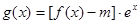 ,若函数
,若函数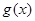 在
在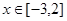 上单调,求实数
上单调,求实数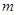 的取值范围.
的取值范围.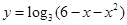 的单调减区间为 ( )
的单调减区间为 ( )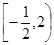
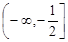

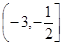
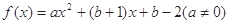 ,若存在实数
,若存在实数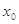 ,使
,使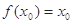 成立,则称
成立,则称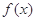 的不动点.
的不动点.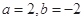 时,求
时,求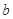 ,函数
,函数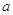 的取值范围;
的取值范围;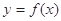 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数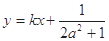 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.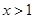 ,则函数
,则函数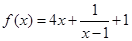 的最小值是( )
的最小值是( )