题目内容
【题目】已知函数![]() (
(![]() )在
)在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(1)求![]() 的值并讨论函数
的值并讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(2)若函数![]() (
(![]() 为常数)有两个零点
为常数)有两个零点![]() (
(![]() )
)
①求实数![]() 的取值范围;
的取值范围;
②求证: ![]()
【答案】(1)见解析;(2)①![]() ;②见解析.
;②见解析.
【解析】试题分析:(1)根据切线的斜率可知在![]() 处的导数,从而求出
处的导数,从而求出![]() 的值,再根据导数的正负讨论函数的单调区间即可;(2)①根据函数有两个零点知,函数的最小值要小于0即可求出;②设
的值,再根据导数的正负讨论函数的单调区间即可;(2)①根据函数有两个零点知,函数的最小值要小于0即可求出;②设![]() ,构造函数
,构造函数![]() (
(![]() ),利用导数确定函数单调性,再根据
),利用导数确定函数单调性,再根据![]() 即可求证.
即可求证.
试题解析:
(1)![]() ,
,
![]() ,∴
,∴![]() .
.
∴![]()
令![]() ,
,
则![]()
∴![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() .
.
则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴在![]() 时,
时, ![]() ,
,
即![]() 时,
时, ![]() ,
,
∴函数![]() 在
在![]() 上单调递减.
上单调递减.
(2)①由条件可知, ![]() ,
,
则![]()
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
要使函数有两个零点,则![]()
∴![]() .
.
②证明:由①可知![]() ,∴
,∴![]() ,
,
又![]() 是两个零点
是两个零点
∴![]()
令![]() (
(![]() )
)
则![]() ,
,
∴![]()
即![]()
又![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]()

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (小时)和销售量
(小时)和销售量![]() (件)的关系作了统计,得到了如下数据并研究.
(件)的关系作了统计,得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中销售量![]() 的平均数和中位数;
的平均数和中位数;
(2)① 作出散点图,并判断变量![]() 与
与![]() 是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程
是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程![]() ;
;
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件,则认为得到的线性回归方程是理想的,试问:①中的线性回归方程是否理想.
附:线性回归方程![]() 中,
中, 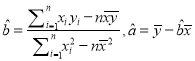 .
.
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记x表示1台机器在三年使用期内的维修次数,y表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() =10,求y与x的函数解析式;
=10,求y与x的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求n的最小值;
”的频率不小于0.8,求n的最小值;
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?