Question

【题目】已知函数.

（1）讨论函数在上的单调性；

（2）是否存在正实数，使与的图象有唯一一条公切线，若存在，求出的值，若不存在，请说明理由.

Answer 1

【答案】（1）当时，在区间上单调递减；当时，在上单调递减；在上单调递增；（2）存在，

【解析】

（1）对函数进行求导，对参数进行分类讨论，即可容易求得函数的单调性；

（2）利用导数的几何意义求得在任意一点处的切线方程，求得方程组，根据方程有唯一解，利用导数根据函数单调性，即可求得.

(1)，

当时，，所以，函数在上单调递减；

当时，由得，由得，

所以，函数在上单调递减；函数在上单调递增.

(2)函数在点处的切线方程为

，即；

函数在点处的切线方程为

，即

由与的图象有唯一一条公切线，

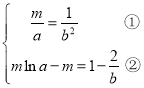∴，由①得代入②消去，

整理得 ③

则此关于的方程③有唯一解，

令，

令，

由得；由得所以，函数在上单调递增，在上单调递减，

则，

（i）当时，二次函数在上显然有一个零点，

时，由方程可得

而所以

则

所以二次函数在上也有一个零点，不合题意.

综上，.

所以存在正实数，使与的图象有唯一一条公切线.