Question

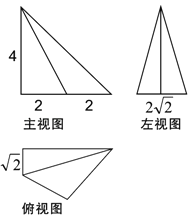
【题目】某几何体的三视图如图所示，则该几何体的外接球的表面积为（ ）

A. 136π B. 144π C. 36π D. 34π

Answer 1

【答案】D

【解析】分析：作出几何体的直观图，建立空间直角坐标系，求出外接球的球心，从而可的外接球的半径，再计算出外接球的面积．

详解：由三视图可知几何体为四棱锥E﹣ABCD，直观图如图所示：

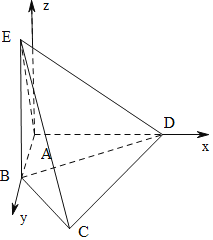
其中，BE⊥平面ABCD，BE=4，AB⊥AD，AB=，

C到AB的距离为2，C到AD的距离为2，

以A为原点，以AB，AD，及平面ABCD过A的垂线为坐标轴建立空间直角坐标系A﹣xyz，

则A（0，0，0），B（0，，0），C（2，2，0），D（4，0，0），E（0，，4）．

设外接球的球心为M（x，y，z），则MA=MB=MC=MD=ME，

∴x2+y2+z2=x2+（y﹣）2+z2=（x﹣2）2+（y﹣2）2+z2=（x﹣4）2+y2+z2=x2+（y﹣）2+（z﹣4）2，

解得x=2，y=，z=2．

∴外接球的半径r=MA==，

∴外接球的表面积S=4πr2=34π．

故选：D．