题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以原点
为参数).在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】分析:解法一:(1)消去参数可得![]() 的普通方程为
的普通方程为![]() ,则极坐标方程为
,则极坐标方程为![]() .极坐标方程化为直角坐标方程可得
.极坐标方程化为直角坐标方程可得![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)设![]() 的极坐标分别为
的极坐标分别为![]() ,则
,则![]() ,联立极坐标方程可得
,联立极坐标方程可得![]() , 则
, 则![]() ,结合三角函数的性质计算可得
,结合三角函数的性质计算可得![]() .
.
解法二: (1)同解法一
(2)曲线![]() 表示圆心为
表示圆心为![]() 且半径为1的圆.联立直线参数方程的标准形式与圆的方程可得
且半径为1的圆.联立直线参数方程的标准形式与圆的方程可得![]() ,结合参数的几何意义知
,结合参数的几何意义知![]() , 则
, 则![]()
解法三: (1)同解法一
(2)曲线![]() 表示圆心为
表示圆心为![]() 且半径为1的圆.
且半径为1的圆. ![]() 的普通方程为
的普通方程为![]() , 由弦长公式可得
, 由弦长公式可得![]() ,则
,则![]() 是等边三角形,
是等边三角形,![]() ,
, ![]() .
.
详解:解法一:(1)由![]() 得
得![]() 的普通方程为
的普通方程为![]() ,
,
又因为![]() , 所以
, 所以![]() 的极坐标方程为
的极坐标方程为![]() .
.
由![]() 得
得![]() ,即
,即![]() ,
,
所以![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)设![]() 的极坐标分别为
的极坐标分别为![]() ,则
,则![]()
由![]() 消去
消去![]() 得
得![]() ,
,
化为![]() ,即
,即![]() ,
,
因为![]() ,即
,即![]() ,所以
,所以![]() ,或
,或![]() ,
,
即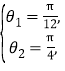 或
或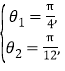 所以
所以![]() .
.
解法二: (1)同解法一
(2)曲线![]() 的方程可化为
的方程可化为![]() ,表示圆心为
,表示圆心为![]() 且半径为1的圆.
且半径为1的圆.
将![]() 的参数方程化为标准形式
的参数方程化为标准形式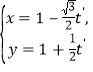 (其中
(其中![]() 为参数),代入
为参数),代入![]() 的直角坐标方程为
的直角坐标方程为![]() 得,
得,![]() ,
,
整理得,![]() ,解得
,解得![]() 或
或![]() .
.
设![]() 对应的参数分别为
对应的参数分别为![]() ,则
,则![]() .所以
.所以![]() ,
,
又因为![]() 是圆
是圆![]() 上的点,所以
上的点,所以![]()
解法三: (1)同解法一
(2)曲线![]() 的方程可化为
的方程可化为![]() ,表示圆心为
,表示圆心为![]() 且半径为1的圆.
且半径为1的圆.
又由①得![]() 的普通方程为
的普通方程为![]() ,
,
则点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]() ,所以
,所以![]() 是等边三角形,所以
是等边三角形,所以![]() ,
,
又因为![]() 是圆
是圆![]() 上的点,所以
上的点,所以![]() .
.

【题目】某中学为了解高一年级学生身高发育情况,对全校![]() 名高一年级学生按性别进行分层抽样检查,测得身高(单位:
名高一年级学生按性别进行分层抽样检查,测得身高(单位:![]() )频数分布表如表
)频数分布表如表![]() 、表
、表![]() .
.
表![]() :男生身高频数分布表
:男生身高频数分布表
身高/ |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
表![]() :女生身高频数分布表
:女生身高频数分布表
身高/ |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)求该校高一女生的人数;
(2)估计该校学生身高在![]() 的概率;
的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出![]() 人,设
人,设![]() 表示身高在
表示身高在![]() 学生的人数,求
学生的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
