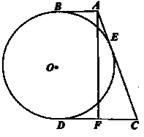
题目内容
切线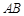 与圆切于点
与圆切于点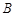 ,圆内有一点
,圆内有一点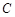 满足
满足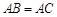 ,
,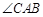 的平分线
的平分线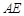 交圆于
交圆于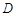 ,
,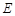 ,延长
,延长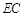 交圆于
交圆于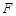 ,延长
,延长 交圆于
交圆于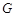 ,连接
,连接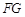 .
.
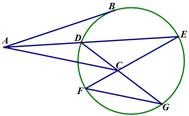
(Ⅰ)证明: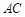 //
//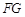 ;
;
(Ⅱ)求证: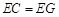 .
.
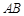 与圆切于点
与圆切于点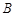 ,圆内有一点
,圆内有一点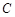 满足
满足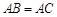 ,
,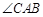 的平分线
的平分线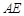 交圆于
交圆于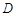 ,
,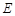 ,延长
,延长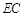 交圆于
交圆于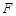 ,延长
,延长 交圆于
交圆于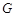 ,连接
,连接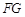 .
.
(Ⅰ)证明:
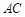 //
//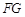 ;
;(Ⅱ)求证:
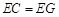 .
.(Ⅰ)详见解析;(Ⅱ)详见解析.
试题分析:(Ⅰ)证明:
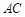 //
//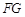 ,只需证明
,只需证明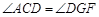 ,而
,而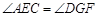 ,即证
,即证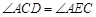 ,只需证△
,只需证△ ∽△
∽△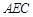 ,即可,由已知切线
,即可,由已知切线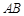 与圆切于点
与圆切于点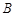 ,圆内有一点
,圆内有一点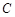 满足
满足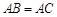 ,
,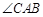 的平分线
的平分线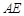 交圆于
交圆于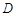 ,
,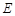 ,由切割线定理知
,由切割线定理知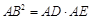 ,从而得
,从而得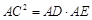 ,故△
,故△ ∽△
∽△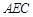 ,从而得证;(Ⅱ)连接
,从而得证;(Ⅱ)连接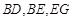 ,求证:
,求证: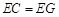 ,注意到△
,注意到△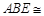 △
△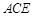 ,可得
,可得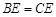 ,只需证
,只需证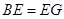 ,即证
,即证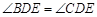 ,即证△
,即证△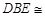 △
△ ,这容易证出.
,这容易证出.试题解析:(Ⅰ)证明:∵
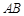 切圆于
切圆于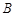 ,∴
,∴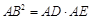 ,又∵
,又∵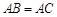 ,∴
,∴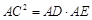 ,∴△
,∴△ ∽△
∽△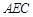 ,∴
,∴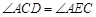 ,又∵
,又∵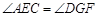 ,∴
,∴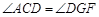 ,∴
,∴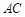 //
//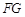 ;
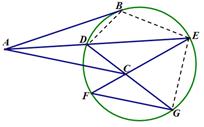
;
(Ⅱ)证明:连接
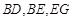 ,由
,由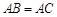 ,
,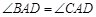 及
及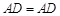 ,知△
,知△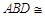 △
△ ,同理有△
,同理有△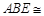 △
△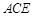 ,∴
,∴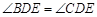 ,故
,故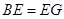 ,又
,又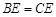 ,∴
,∴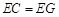 .
.
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
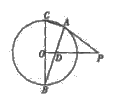
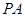 与圆
与圆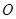 相切于点
相切于点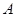 ,直径
,直径 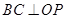 ,连结
,连结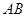 交
交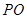 于点
于点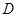 .
.
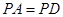 ;
;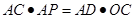 .
.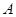 、
、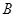 、
、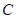 是圆
是圆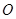 上三点,
上三点,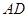 是
是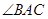 的角平分线,交圆
的角平分线,交圆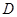 ,过
,过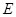 .
.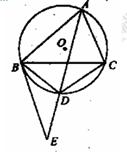
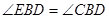 ;
;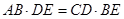 .
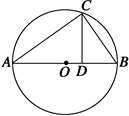
.
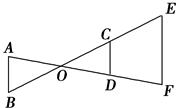
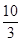 cm
cm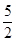 cm
cm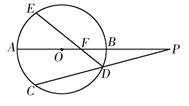
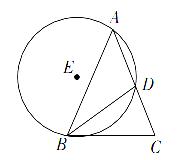
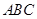 中,
中,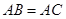 ,
,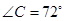 ,圆
,圆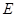 过
过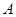 、
、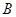 两点且与
两点且与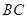 相切于点
相切于点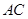 交于点
交于点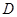 ,连结
,连结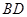 ,若
,若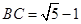 ,则
,则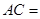 .
.
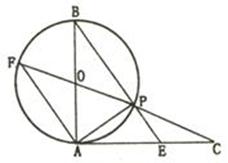
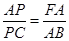 ;
; 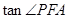 的值.
的值.