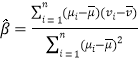题目内容
【题目】某老师是省级课题组的成员,主要研究课堂教学目标达成度,为方便研究,从实验班中随机抽取30次的随堂测试成绩进行数据分析![]() 已知学生甲的30次随堂测试成绩如下
已知学生甲的30次随堂测试成绩如下![]() 满分为100分
满分为100分![]() :
:
88 58 50 36 75 39 57 62 72 51
85 39 57 53 72 46 64 74 53 50
44 83 70 63 71 64 54 62 61 42
![]() 把学生甲的成绩按
把学生甲的成绩按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,列出频率分布表,并画出频率分布直方图;
分成6组,列出频率分布表,并画出频率分布直方图;
![]() 为更好的分析学生甲存在的问题,从随堂测试成绩50分以下
为更好的分析学生甲存在的问题,从随堂测试成绩50分以下![]() 不包括50分
不包括50分![]() 的试卷中随机抽取3份进行分析,求恰有2份成绩在
的试卷中随机抽取3份进行分析,求恰有2份成绩在![]() 内的概率.
内的概率.
【答案】(1)见解析(2)![]()
【解析】
![]() 先作出频率分布表,由此能画出频率分布直方图.
先作出频率分布表,由此能画出频率分布直方图.
![]() 成绩在
成绩在![]() 内的有3个数据,记为A,B,C,成绩在
内的有3个数据,记为A,B,C,成绩在![]() 内的有3个数据,记为a,b,c,从
内的有3个数据,记为a,b,c,从![]() ,
,![]() 共6个数据中任意抽取3个,利用列举法能求出恰有2份成绩在
共6个数据中任意抽取3个,利用列举法能求出恰有2份成绩在![]() 内的概率.
内的概率.
解:![]() 频率分布表为:
频率分布表为:
分组 | 频数累计 | 频率 |
| 3 |
|
| 3 |
|
| 9 |
|
| 6 |
|
| 6 |
|
| 3 |
|
合计 | 30 | 1 |
画出频率分布直方图如下:
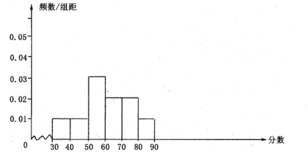
![]() 成绩在
成绩在![]() 内的有3个数据,记为A,B,C,
内的有3个数据,记为A,B,C,
成绩在![]() 内的有3个数据,记为a,b,c,
内的有3个数据,记为a,b,c,
则从![]() ,
,![]() 共6个数据中任意抽取3个,基本事件有20个,分别为:
共6个数据中任意抽取3个,基本事件有20个,分别为:
![]() B,
B,![]() ,
,![]() B,
B,![]() ,
,![]() B,
B,![]() ,
,![]() B,
B,![]() ,
,![]() C,
C,![]() ,
,![]() C,
C,![]() ,
,![]() C,
C,![]() ,
,![]() C,
C,![]() ,
,![]() C,
C,![]() ,
,![]() C,
C,![]() ,
,![]() a,
a,![]() ,
,![]() a,
a,![]() ,
,![]() b,
b,![]() ,
,![]() a,
a,![]() ,
,![]() a,
a,![]() ,
,![]() b,
b,![]() ,
,![]() a,
a,![]() ,
,![]() a,
a,![]() ,
,![]() b,
b,![]() ,
,![]() b,
b,![]() ,
,
其中恰好有两份成绩在![]() 内共有9个,
内共有9个,
![]() 恰有2份成绩在
恰有2份成绩在![]() 内的概率
内的概率![]() .
.

【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司底薪70元,每单抽成2元;乙公司无底薪,40单以内(含40单)的部分每单抽成4元,超出40单的部分每单抽成6元.假设同一公司的送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 20 | 20 | 40 | 10 |
(1)现从甲公司记录的这100天中随机抽取两天,求这两天送餐单数都大于40的概率;
(2)若将频率视为概率,回答以下问题:
(i)记乙公司送餐员日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)小明拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.