题目内容
15.在△ABC中,三个内角A,B,C的对边分别是a,b,c,其中b=5,c=3且满足sin22A-sin2AsinA+cos2A=1.求:(1)cos(B-C)的值;
(2)O为△ABC的外心,若$\overrightarrow{OA}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,求m+n的值.
分析 (1)根据三角函数的倍角公式进行化简,结合正弦定理和两角和差的余弦公式即可cos(B-C)的值;
(2)建立平面坐标系,求出外接圆的圆心坐标,利用向量的基本定理建立方程关系即可得到结论.
解答 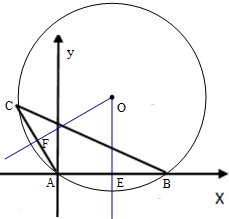 解:(1)由sin22A-sin2AsinA+cos2A=1得:
解:(1)由sin22A-sin2AsinA+cos2A=1得:
sin22A-sin2AsinA+1-2sin2A=1,
即sin22A-sin2AsinA-2sin2A=0,
即(sin2A+sinA)(sin2A-2sinA)=0
即(2sinAcosA+sinA)(2sinAcosA-2sinA)=0,
∴(2cosA+1)(2cosA-2)=0,
解得cosA=$-\frac{1}{2}$或cosA=1(舍),
∴A=$\frac{2π}{3}$,
在△ABC中,由余弦定理得:a2=b2+c2-2bccosA=25+9-2×5×3×$(-\frac{1}{2})$=49,则a=7,
在△ABC中,由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$,得$sinB=\frac{5\sqrt{3}}{14}$,
sinC=$\frac{3\sqrt{3}}{14}$,
则cosB=$\frac{11}{14}$,cosC=$\frac{13}{14}$,
则cos(B-C)=cosBcosC+sinBsinC=$\frac{11}{14}$×$\frac{13}{14}$+$\frac{5\sqrt{3}}{14}$×$\frac{3\sqrt{3}}{14}$=$\frac{47}{49}$.
(2)建立直角坐标系得A(0,0),B(5,0),C($-\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$),
则AB的中垂线为x=$\frac{5}{2}$,即O的横坐标为$\frac{5}{2}$,
AC的斜率k=-$\sqrt{3}$,AC的中点F($-\frac{3}{4}$,$\frac{3\sqrt{3}}{4}$),
则AC的中垂线的斜率k=$\frac{\sqrt{3}}{3}$,中垂线方程为y-$\frac{3\sqrt{3}}{4}$=$\frac{\sqrt{3}}{3}$(x+$\frac{3}{4}$),
令x=$\frac{5}{2}$,解得y=$\frac{11\sqrt{3}}{6}$,
即O($\frac{5}{2}$,$\frac{11\sqrt{3}}{6}$)
由$\overrightarrow{OA}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,得(-$\frac{5}{2}$,-$\frac{11\sqrt{3}}{6}$)=m(5,0)+n($-\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$),
即$\left\{\begin{array}{l}{5m-\frac{3}{2}n=-\frac{5}{2}}\\{\frac{3\sqrt{3}}{2}n=-\frac{11\sqrt{3}}{6}}\end{array}\right.$,解得m=$-\frac{2}{3}$,n=$-\frac{11}{9}$,
则m+n=$-\frac{2}{3}$$-\frac{11}{9}$=-$\frac{17}{9}$.
点评 本题主要考查解三角形的应用以及平面向量的基本定理的应用,建立坐标系,利用向量法是解决本题的关键.

| A. | 2 | B. | -2 | C. | ±2 | D. | $\sqrt{5}$ |
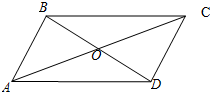 如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.
如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.