题目内容
8.不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤1}\end{array}\right.$表示的平面区域的面积为( )| A. | 1 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 先作出不等式组对应的平面区域,然后根据区域确定面积即可.
解答 解:作出不等式组对应的平面区域,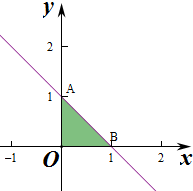
则A(0,1),B(1,0),
则三角形的面积S=$\frac{1}{2}×1×1$=$\frac{1}{2}$,
故选:D.
点评 本题主要考查不等式组表示的平面区域,利用二元一次不等式组表示平面区域,作出不等式组对应的区域是解决本题的关键,然后根据相应的面积公式进行求解.

练习册系列答案
相关题目
18.已知复数z满足z=$\frac{(1+i)(2-i)}{i}$(i为虚数单位),则$\overline{z}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.设a1,a2,…an是正整数1,2,3,…,n的一个排列,令bj表示排在j的左边且比j大的数的个数,称为j的逆序数.如在排列3,5,1,4,2,6中,5的逆序数是0,2的逆序数是3,则由1至8这8个数字构成的所有排列中,满足1的逆序数是2,2的逆序数是3,5的逆序数是3的不同排列种数是( )
| A. | 144 | B. | 172 | C. | 180 | D. | 192 |
13.下列说法中正确的序号为( )
| A. | 若直线l平行于平面α内的无数条直线,则l∥α; | |
| B. | 若α∥β,a?α,b?β,则a与b是异面直线; | |
| C. | 若α∥β,a?α,则a∥β; | |
| D. | 若α∩β=b,a?α,则a与β一定相交. |
20.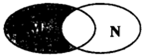 已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )
已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )
 已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )
已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )| A. | {x|0<x<1} | B. | {x|0<x≤1} | C. | {x|1<x<2} | D. | {x|2<x<3} |
17.若向量$\overrightarrow{a}$=(3,4),且存在实数x,y,使得$\overrightarrow{a}$=x$\overrightarrow{{e}_{1}}+y\overrightarrow{{e}_{2}}$,则$\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}$可以是( )
| A. | $\overrightarrow{{e}_{1}}$=(0,0),$\overrightarrow{{e}_{2}}$=(-1,2) | B. | $\overrightarrow{{e}_{1}}$=(-1,3),$\overrightarrow{{e}_{2}}$=(2,-6) | ||
| C. | $\overrightarrow{{e}_{1}}$=(-1,2),$\overrightarrow{{e}_{2}}$=(3,-1) | D. | $\overrightarrow{{e}_{1}}$=(-$\frac{1}{2}$,1),$\overrightarrow{{e}_{2}}$=(1,-2) |
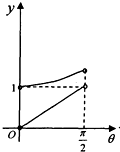
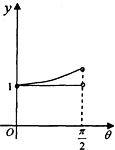
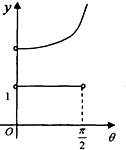
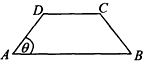 如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,$\frac{π}{2}$),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,设e1=f(θ),e1e2=g(θ),则f(θ),g(θ)的大致图象是( )
如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,$\frac{π}{2}$),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,设e1=f(θ),e1e2=g(θ),则f(θ),g(θ)的大致图象是( )