题目内容
3.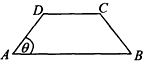 如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,$\frac{π}{2}$),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,设e1=f(θ),e1e2=g(θ),则f(θ),g(θ)的大致图象是( )
如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,$\frac{π}{2}$),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,设e1=f(θ),e1e2=g(θ),则f(θ),g(θ)的大致图象是( )| A. | 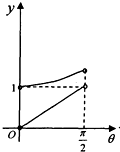 | B. | 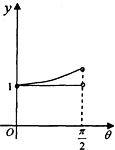 | C. |  | D. | 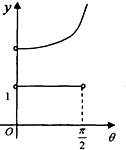 |
分析 用特殊值法,当θ→0时,e1→2,e1e2=1,根据图象可得结论.
解答 解:用特殊值法,当θ→0时,e1→2,e1e2=1,根据图象,C符合.
故选:C.
点评 本题主要考查椭圆和双曲线的离心率的表示,考查考生对圆锥曲线的性质的应用,圆锥曲线是高考的重点每年必考,平时要注意基础知识的积累和练习.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
14.若抛物线y2=mx的准线经过双曲线x2-$\frac{{y}^{2}}{3}$=1的一个焦点,则负数m等于( )
| A. | -1 | B. | -2 | C. | -4 | D. | -8 |
8.不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤1}\end{array}\right.$表示的平面区域的面积为( )
| A. | 1 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
6.如果cos(3π-α)=$\frac{4}{5}$,且α是第三象限的角,则sin2α=( )
| A. | $\frac{7}{25}$ | B. | $\frac{24}{25}$ | C. | -$\frac{12}{25}$ | D. | -$\frac{24}{25}$ |
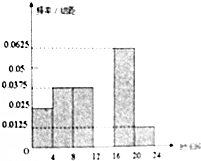 上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题:
上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题: