题目内容
16.设a1,a2,…an是正整数1,2,3,…,n的一个排列,令bj表示排在j的左边且比j大的数的个数,称为j的逆序数.如在排列3,5,1,4,2,6中,5的逆序数是0,2的逆序数是3,则由1至8这8个数字构成的所有排列中,满足1的逆序数是2,2的逆序数是3,5的逆序数是3的不同排列种数是( )| A. | 144 | B. | 172 | C. | 180 | D. | 192 |
分析 由题意知1必在第3位,2必在第5位; 5可以在第6位,5也可以在第7位,5也可以在第8位;分3种情况进行讨论.
解答 解:由题意知,1必在第3位,2必在第5位; 5可以在第6位,5可以在第7位,5在第8位.
若5在第6位,则5前面有3个空位,需从6,7,8中选出3个填上,
把剩下的2个数填在5后面的2个空位上,则有A33A22=12种,
若5在第7位,则5前面有4个空位,其中3,4当中的一个应填在其中的一个空位上,余下3个空位,需从6,7,8中选出3个填上则有C21A44=48种,
若5在第8位,则5前面有5个空位,则有A55=120种,
合计为:12+48+120=180种,
故选:C.
点评 本题考查排列、组合及简单计数问题的应用,体现了分类讨论的数学思想,本题解题的关键是分类时做到不重不漏.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.已知平面向量$\overrightarrow{a}$、$\overrightarrow{b}$,|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2$\sqrt{3}$且$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$垂直,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
4.已知M(a,5-a,2a-1),N(1,a+2,2-a)两点,当|MN|取得最小值时,a的值是( )
| A. | 19 | B. | $\frac{19}{14}$ | C. | -$\frac{8}{7}$ | D. | $\frac{8}{7}$ |
8.不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤1}\end{array}\right.$表示的平面区域的面积为( )
| A. | 1 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
5.已知直线l1:3x+4y-12=0,l2:7x+y-28=0,则直线l1与l2的夹角是( )
| A. | 30° | B. | 45° | C. | 135° | D. | 150° |
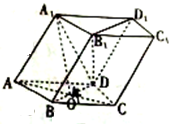 在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.
在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.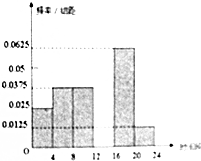 上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题:
上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题: