题目内容
如图,已知位于y轴左侧的圆C与y轴相切于点(0,1)且被x轴分成的两段圆弧长之比为1:2,过点H(0,t)的直线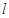 于圆C相交于M、N两点,且以MN为直径的圆恰好经过坐标原点O。
于圆C相交于M、N两点,且以MN为直径的圆恰好经过坐标原点O。
(1) 求圆C的方程;
(2) 当t=1时,求出直线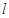 的方程;
的方程;
(3) 求直线OM的斜率k的取值范围。
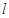 于圆C相交于M、N两点,且以MN为直径的圆恰好经过坐标原点O。
于圆C相交于M、N两点,且以MN为直径的圆恰好经过坐标原点O。(1) 求圆C的方程;
(2) 当t=1时,求出直线
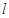 的方程;
的方程;(3) 求直线OM的斜率k的取值范围。
解 (1)因为位于
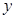 轴左侧的圆
轴左侧的圆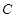 与
与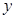 轴相切于点
轴相切于点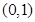 ,所以圆心
,所以圆心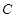 在直线
在直线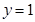 上,
上,设圆
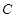 与
与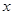 轴的交点分别为
轴的交点分别为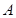 、
、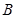 ,
,由圆
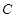 被
被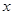 轴分成的两段弧长之比为
轴分成的两段弧长之比为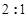 ,得
,得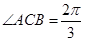 ,
,所以
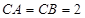 ,圆心
,圆心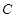 的坐标为
的坐标为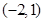 ,
,所以圆
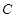 的方程为:
的方程为: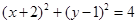 . …………………4分
. …………………4分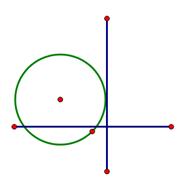
(2)当
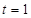 时,由题意知直线
时,由题意知直线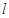 的斜率存在,设直线
的斜率存在,设直线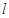 方程为
方程为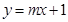 ,
,由
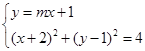 得
得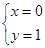 或
或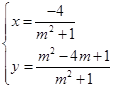 ,
,不妨令
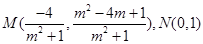 ,
,因为以
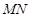 为直径的圆恰好经过
为直径的圆恰好经过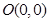 ,
,所以
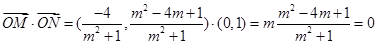 ,
,解得
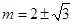 ,所以所求直线
,所以所求直线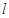 方程为
方程为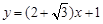 或
或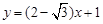 .…………10分
.…………10分(3)设直线
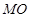 的方程为
的方程为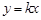 ,
,由题意知,
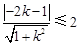 ,解之得
,解之得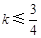 ,
,同理得,
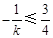 ,解之得
,解之得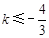 或
或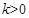 . 由(2)知,
. 由(2)知,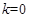 也满足题意.
也满足题意.所以
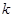 的取值范围是
的取值范围是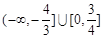 . …………16分
. …………16分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
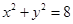 内有一点
内有一点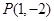 ,
,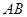 为过点
为过点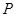 且倾斜角为
且倾斜角为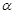 的弦,
的弦,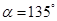 时,求弦
时,求弦 的直线被圆
的直线被圆 所截得的弦长为
所截得的弦长为



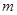 =0与圆x2+y2+x-2y=0相交于P、Q两点,O为坐
=0与圆x2+y2+x-2y=0相交于P、Q两点,O为坐 标原点,若OP
标原点,若OP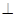 OQ,求
OQ,求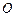 为平面直角坐标系的原点,过点
为平面直角坐标系的原点,过点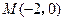 的直线
的直线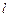 与圆
与圆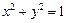 交于
交于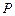 ,
,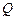 两点.
两点.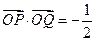 ,求直线
,求直线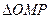 与
与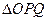 的面积相等,求直线
的面积相等,求直线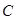 :
: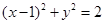 ,过点
,过点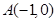 的直线
的直线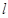 将圆
将圆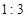 的两段圆弧,则直线
的两段圆弧,则直线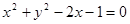 关于直线
关于直线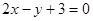 对称的圆的方程是 __
对称的圆的方程是 __ 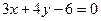 被圆
被圆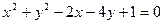 截得的弦长为 .
截得的弦长为 .