题目内容
(本小题9分)设直线3x+y+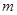 =0与圆x2+y2+x-2y=0相交于P、Q两点,O为坐
=0与圆x2+y2+x-2y=0相交于P、Q两点,O为坐 标原点,若OP
标原点,若OP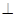 OQ,求
OQ,求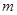 的值.
的值.
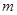 =0与圆x2+y2+x-2y=0相交于P、Q两点,O为坐
=0与圆x2+y2+x-2y=0相交于P、Q两点,O为坐 标原点,若OP
标原点,若OP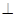 OQ,求
OQ,求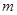 的值.
的值.解:由3x+y+m=0得: y=-3x-m 代入圆方程得: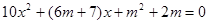
设P、Q两点坐标为P(x1,y1)、Q(x2,y2) 则x1 +x2=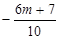 x1×x2=
x1×x2=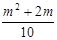
∵OP⊥OQ ∴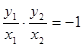 即x1×x2+ y1×y2=0∴ x1×x2+(-3x1-m) (-3x2-m) =0
即x1×x2+ y1×y2=0∴ x1×x2+(-3x1-m) (-3x2-m) =0
整理得:10x1×x2+3 m (x1 +x2)+ m2="0 " ∴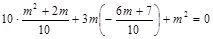
解得:m=0或m=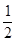 又△=(6m+7)2-40(m2+2m)= -4m2+4m+49
又△=(6m+7)2-40(m2+2m)= -4m2+4m+49
当m=0时,△>0;当m=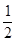 时,△>0;∴m=0或m=
时,△>0;∴m=0或m=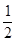
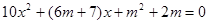
设P、Q两点坐标为P(x1,y1)、Q(x2,y2) 则x1 +x2=
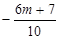 x1×x2=
x1×x2=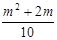
∵OP⊥OQ ∴
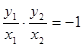 即x1×x2+ y1×y2=0∴ x1×x2+(-3x1-m) (-3x2-m) =0
即x1×x2+ y1×y2=0∴ x1×x2+(-3x1-m) (-3x2-m) =0整理得:10x1×x2+3 m (x1 +x2)+ m2="0 " ∴
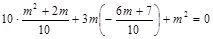
解得:m=0或m=
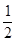 又△=(6m+7)2-40(m2+2m)= -4m2+4m+49
又△=(6m+7)2-40(m2+2m)= -4m2+4m+49当m=0时,△>0;当m=
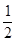 时,△>0;∴m=0或m=
时,△>0;∴m=0或m=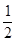
略

练习册系列答案
相关题目
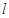 于圆C相交于M、N两点,且以MN为直径的圆恰好经过坐标原点O。
于圆C相交于M、N两点,且以MN为直径的圆恰好经过坐标原点O。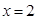 被圆
被圆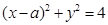 所截得的弦长等于
所截得的弦长等于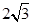 ,则
,则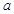 的值为
的值为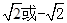
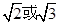
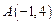 的圆的圆心为
的圆的圆心为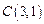 .
.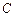 的方程;
的方程;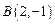 的直线
的直线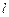 被圆
被圆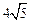 ,求直线
,求直线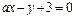 与圆
与圆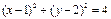 相交于
相交于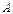 、
、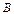 两点,且弦
两点,且弦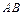 的长为
的长为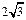 ,则
,则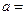 ____________.
____________.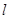 与圆
与圆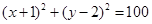 相交于
相交于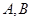 两点,弦
两点,弦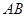 的中点为
的中点为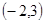 ,则直线
,则直线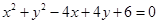 截直线
截直线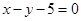 所得的弦长为 。
所得的弦长为 。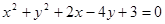
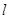 与圆C相切,且在
与圆C相切,且在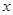 轴、
轴、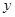 轴上的截距相等,求直线
轴上的截距相等,求直线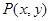 向圆引一条切线,切点为M,O为坐标原点,且有
向圆引一条切线,切点为M,O为坐标原点,且有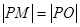 ,求点P的轨迹方程.
,求点P的轨迹方程.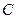 的圆心在
的圆心在
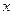 轴的正半轴上,且圆
轴的正半轴上,且圆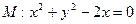 相外切,又和直线
相外切,又和直线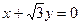 相切,求圆
相切,求圆 程。
程。