题目内容
.(本小题满分16分)
已知函数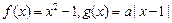 .
.
(1)若关于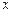 的方程
的方程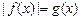 只有一个实数解,求实数
只有一个实数解,求实数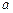 的取值范围;
的取值范围;
(2)若当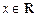 时,不等式
时,不等式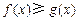 恒成立,求实数
恒成立,求实数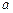 的取值范围;
的取值范围;
(3)求函数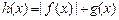 在区间
在区间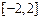 上的最大值(直接写出结果,不需给出演算步骤).
上的最大值(直接写出结果,不需给出演算步骤).
已知函数
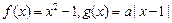 .
.(1)若关于
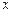 的方程
的方程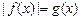 只有一个实数解,求实数
只有一个实数解,求实数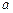 的取值范围;
的取值范围;(2)若当
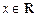 时,不等式
时,不等式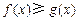 恒成立,求实数
恒成立,求实数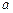 的取值范围;
的取值范围;(3)求函数
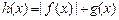 在区间
在区间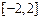 上的最大值(直接写出结果,不需给出演算步骤).
上的最大值(直接写出结果,不需给出演算步骤).(1)方程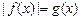 ,即
,即 ,变形得
,变形得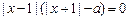 ,
,
显然,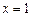 已是该方程的根,从而欲原方程只有一解,即要求方程
已是该方程的根,从而欲原方程只有一解,即要求方程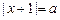 ,
,
有且仅有一个等于1的解或无解 ,
结合图形得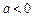 . ……………………4分
. ……………………4分
(2)不等式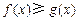 对
对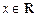 恒成立,即
恒成立,即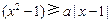 (*)对
(*)对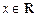 恒成立,
恒成立,
①当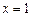 时,(*)显然成立,此时
时,(*)显然成立,此时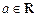 ;
;
②当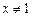 时,(*)可变形为
时,(*)可变形为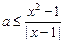 ,令
,令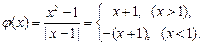
因为当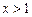 时,
时,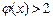 ,当
,当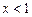 时,
时,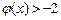 ,
,
所以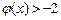 ,故此时
,故此时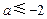 .
.
综合①②,得所求实数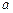 的取值范围是
的取值范围是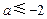 . ………………………8分
. ………………………8分
(3)因为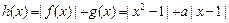 =
=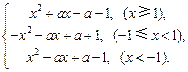 …10分
…10分
① 当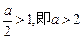 时,结合图形可知
时,结合图形可知 在
在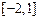 上递减,在
上递减,在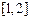 上递增,
上递增,
且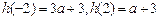 ,经比较,此时
,经比较,此时 在
在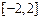 上的最大值为
上的最大值为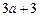 .
.
② 当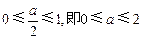 时,结合图形可知
时,结合图形可知 在
在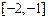 ,
,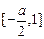 上递减,
上递减,
在 ,
,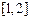 上递增,且
上递增,且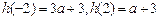 ,
,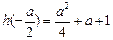 ,
,
经比较,知此时 在
在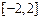 上的最大值为
上的最大值为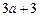 .
.
③ 当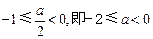 时,结合图形可知
时,结合图形可知 在
在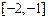 ,
,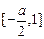 上递减,
上递减,
在 ,
,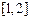 上递增,且
上递增,且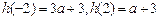 ,
,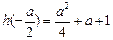 ,
,
经比较,知此时 在
在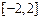 上的最大值为
上的最大值为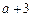 .
.
④ 当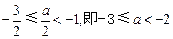 时,结合图形可知
时,结合图形可知 在
在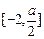 ,
,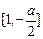 上递减,
上递减,
在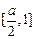 ,
,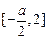 上递增,且
上递增,且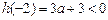 ,
, 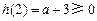 ,
,
经比较,知此时 在
在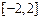 上的最大值为
上的最大值为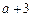 .
.
当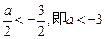 时,结合图形可知
时,结合图形可知 在
在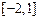 上递减,在
上递减,在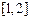 上递增,
上递增,
故此时 在
在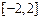 上的最大值为
上的最大值为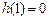 .
.
综上所述,当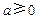 时,
时, 在
在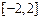 上的最大值为
上的最大值为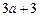 ;
;
当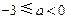 时,
时, 在
在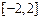 上的最大值为
上的最大值为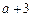 ;
;
当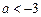 时,
时, 在
在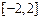 上的最大值为0.………………16分
上的最大值为0.………………16分
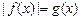 ,即
,即 ,变形得
,变形得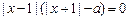 ,
,显然,
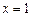 已是该方程的根,从而欲原方程只有一解,即要求方程
已是该方程的根,从而欲原方程只有一解,即要求方程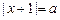 ,
,有且仅有一个等于1的解或无解 ,
结合图形得
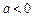 . ……………………4分
. ……………………4分(2)不等式
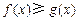 对
对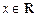 恒成立,即
恒成立,即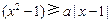 (*)对
(*)对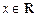 恒成立,
恒成立,①当
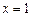 时,(*)显然成立,此时
时,(*)显然成立,此时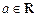 ;
; ②当
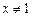 时,(*)可变形为
时,(*)可变形为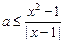 ,令
,令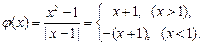
因为当
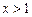 时,
时,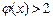 ,当
,当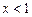 时,
时,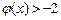 ,
,所以
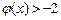 ,故此时
,故此时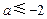 .
. 综合①②,得所求实数
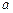 的取值范围是
的取值范围是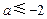 . ………………………8分
. ………………………8分(3)因为
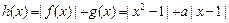 =
=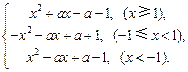 …10分
…10分① 当
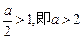 时,结合图形可知
时,结合图形可知 在
在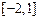 上递减,在
上递减,在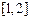 上递增,
上递增,且
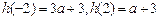 ,经比较,此时
,经比较,此时 在
在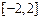 上的最大值为
上的最大值为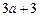 .
.② 当
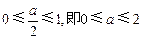 时,结合图形可知
时,结合图形可知 在
在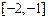 ,
,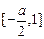 上递减,
上递减,在
 ,
,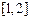 上递增,且
上递增,且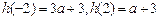 ,
,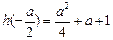 ,
,经比较,知此时
 在
在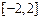 上的最大值为
上的最大值为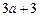 .
.③ 当
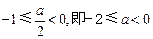 时,结合图形可知
时,结合图形可知 在
在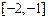 ,
,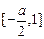 上递减,
上递减,在
 ,
,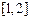 上递增,且
上递增,且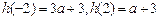 ,
,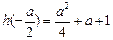 ,
,经比较,知此时
 在
在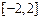 上的最大值为
上的最大值为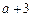 .
.④ 当
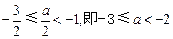 时,结合图形可知
时,结合图形可知 在
在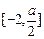 ,
,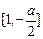 上递减,
上递减,在
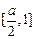 ,
,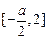 上递增,且
上递增,且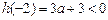 ,
, 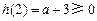 ,
,经比较,知此时
 在
在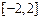 上的最大值为
上的最大值为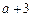 .
.当
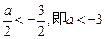 时,结合图形可知
时,结合图形可知 在
在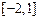 上递减,在
上递减,在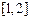 上递增,
上递增,故此时
 在
在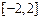 上的最大值为
上的最大值为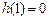 .
.综上所述,当
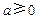 时,
时, 在
在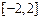 上的最大值为
上的最大值为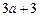 ;
;当
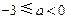 时,
时, 在
在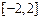 上的最大值为
上的最大值为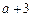 ;
;当
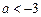 时,
时, 在
在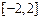 上的最大值为0.………………16分
上的最大值为0.………………16分略

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 则运营的年平均利润最大时,每辆客车营运的年数是 ( )
则运营的年平均利润最大时,每辆客车营运的年数是 ( ) 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.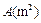 的宿舍楼.已知土地的征用费为2388元/
的宿舍楼.已知土地的征用费为2388元/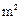 ,且每层的建筑面积相同,土地的征用面积为第一层的2.5倍.经工程技术人员核算,第一.二层的建筑费用都为445元/
,且每层的建筑面积相同,土地的征用面积为第一层的2.5倍.经工程技术人员核算,第一.二层的建筑费用都为445元/ 计这幢宿舍楼的楼高层数,使总费用最小,并求出其最小费用.(总费用为建筑费用和征地费用之和)
计这幢宿舍楼的楼高层数,使总费用最小,并求出其最小费用.(总费用为建筑费用和征地费用之和)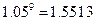 、
、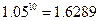 、
、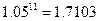 )
)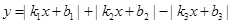 (其中
(其中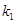 ,
,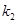 ,
,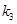 为正实数,
为正实数,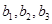 为非零实数)的图象,则根据你所判断的图象,
为非零实数)的图象,则根据你所判断的图象,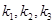 之间一定成立的关系是( )
之间一定成立的关系是( )
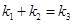 B.
B.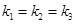 C.
C.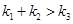 D.
D.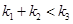
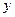 (百件)与销售单价
(百件)与销售单价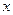 (元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.
(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.