题目内容
16.等比数列{an}前n项的和为2n-1,则数列{an+2}前n项的和为Sn=2n-1+2n.分析 由等比数列{an}前n项的和为2n-1,求得通项an=2n-1,再由分组求和,即可得到所求数列的和.
解答 解:由Sn=2n-1,
可得a1=S1=1,
a2=S2-S1=3-1=2,
则公比为2,
则an=2n-1,
即有数列{an+2}前n项的和Sn=2n-1+2n.
故答案为:2n-1+2n.
点评 本题考查等比数列的求和公式和通项公式的运用,考查数列的分组求和方法,属于基础题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
6.已知实数x、y满足$\left\{\begin{array}{l}{x+y≥2}\\{x-y≤2}\\{0≤y≤3}\end{array}\right.$,则z=2x-y的取值范围是( )
| A. | [-5,7] | B. | [5,7] | C. | [4,7] | D. | [-5,4] |
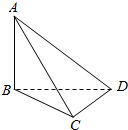 如图,三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,若AB=BC=CD=2,则该三棱锥的侧视图(投影线平行于BD)的面积为$\sqrt{2}$.
如图,三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,若AB=BC=CD=2,则该三棱锥的侧视图(投影线平行于BD)的面积为$\sqrt{2}$.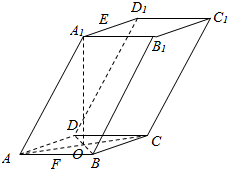 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AB=1,∠DAB=60°,AA1=$\sqrt{3}$,BD中点为O,A1O⊥平面ABCD,E、F分别为A1D1,AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AB=1,∠DAB=60°,AA1=$\sqrt{3}$,BD中点为O,A1O⊥平面ABCD,E、F分别为A1D1,AB的中点.