题目内容
(16分)如图所示,P是抛物线C:y=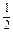 x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.
x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.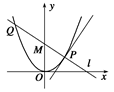
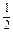 x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.
x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.
点M到x轴的最短距离是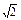 +1
+1
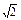 +1
+1 设P(x0,y0),则y0=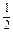 x
x ,
,
∴过点P的切线斜率k=x0,
当x0=0时不合题意,∴x0≠0.
∴直线l的斜率kl=- =-
=-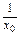 ,
,
∴直线l的方程为y-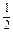 x
x =-
=-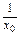 (x-x0).
(x-x0).
此式与y=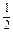 x2联立消去y得
x2联立消去y得
x2+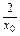 x- x
x- x -2=0.
-2=0.
设Q(x1,y1),M(x,y).∵M是PQ的中点,
∴ ,
,
消去x0,得y=x2+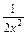 +1(x≠0)就是所求的轨迹方程.由x≠0知x2>0,
+1(x≠0)就是所求的轨迹方程.由x≠0知x2>0,
∴y=x2+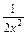 +1≥2
+1≥2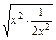 +1=
+1=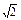 +1.
+1.
上式等号仅当x2=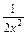 ,即x=±
,即x=±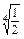 时成立,
时成立,
所以点M到x轴的最短距离是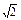 +1.
+1.
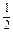 x
x ,
,∴过点P的切线斜率k=x0,
当x0=0时不合题意,∴x0≠0.
∴直线l的斜率kl=-
 =-
=-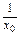 ,
,∴直线l的方程为y-
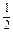 x
x =-
=-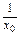 (x-x0).
(x-x0).此式与y=
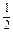 x2联立消去y得
x2联立消去y得x2+
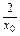 x- x
x- x -2=0.
-2=0.设Q(x1,y1),M(x,y).∵M是PQ的中点,
∴
 ,
,消去x0,得y=x2+
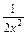 +1(x≠0)就是所求的轨迹方程.由x≠0知x2>0,
+1(x≠0)就是所求的轨迹方程.由x≠0知x2>0,∴y=x2+
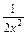 +1≥2
+1≥2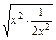 +1=
+1=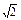 +1.
+1.上式等号仅当x2=
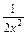 ,即x=±
,即x=±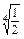 时成立,
时成立,所以点M到x轴的最短距离是
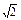 +1.
+1.
练习册系列答案
相关题目
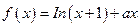 。
。 (I)当
(I)当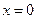 时,函数
时,函数 取得极大值,求实数
取得极大值,求实数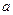 的值;
的值;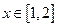 ,使不等式
,使不等式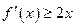 成立,其中
成立,其中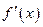 为
为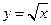 相切的直线方程。
相切的直线方程。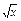 在x=x0处的导数.
在x=x0处的导数.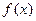 上一点A(1,0)的切线的倾斜角为45°则
上一点A(1,0)的切线的倾斜角为45°则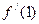 =__________.
=__________. 的值,使曲线
的值,使曲线 与直线
与直线 相切于点
相切于点 .
.