题目内容
(本小题满分14分)已知函数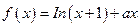 。
。
 (I)当
(I)当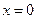 时,函数
时,函数 取得极大值,求实数
取得极大值,求实数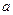 的值;
的值;
(II)若存在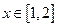 ,使不等式
,使不等式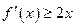 成立,其中
成立,其中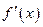 为
为 的导函数,求实数
的导函数,求实数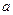 的取值范围;
的取值范围;
(III)求函数 的单调区间。
的单调区间。
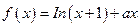 。
。 (I)当
(I)当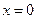 时,函数
时,函数 取得极大值,求实数
取得极大值,求实数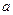 的值;
的值;(II)若存在
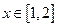 ,使不等式
,使不等式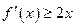 成立,其中
成立,其中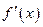 为
为 的导函数,求实数
的导函数,求实数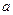 的取值范围;
的取值范围;(III)求函数
 的单调区间。
的单调区间。(I)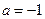
(II)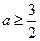
(III)函数 递增区间是
递增区间是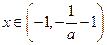 ,递减区间是
,递减区间是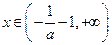
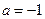
(II)
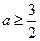
(III)函数
 递增区间是
递增区间是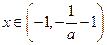 ,递减区间是
,递减区间是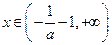
(1)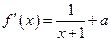 由
由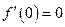 ,得
,得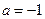 ,此时
,此时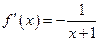
当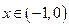 时,
时, ,函数
,函数 在区间
在区间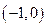 上单调递增;
上单调递增;
当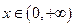 时,
时,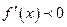 ,
, 函数在区间
函数在区间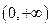 上单调递减;
上单调递减;
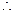
 函数在
函数在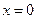 处取得极大值,故
处取得极大值,故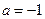 ……………………5分
……………………5分
(2)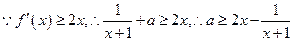
令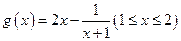
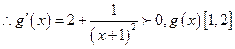 是增函数,
是增函数,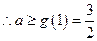 …………10分
…………10分
(3)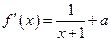
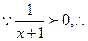 当
当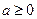 时,
时, ,
, 函数在
函数在 上是增函数。
上是增函数。
当 时,令
时,令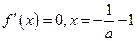
若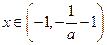 时,
时, ,若
,若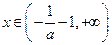 时,
时,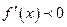
综上,当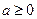 时,函数
时,函数 递增区间是
递增区间是
当 时,函数
时,函数 递增区间是
递增区间是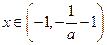 ,递减区间是
,递减区间是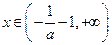 ……13分
……13分
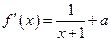 由
由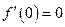 ,得
,得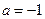 ,此时
,此时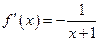
当
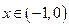 时,
时, ,函数
,函数 在区间
在区间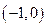 上单调递增;
上单调递增;当
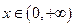 时,
时,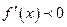 ,
, 函数在区间
函数在区间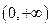 上单调递减;
上单调递减;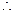
 函数在
函数在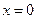 处取得极大值,故
处取得极大值,故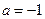 ……………………5分
……………………5分(2)
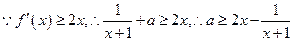
令
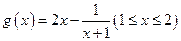
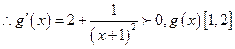 是增函数,
是增函数,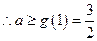 …………10分
…………10分(3)
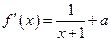
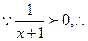 当
当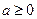 时,
时, ,
, 函数在
函数在 上是增函数。
上是增函数。当
 时,令
时,令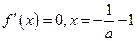
若
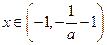 时,
时, ,若
,若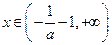 时,
时,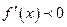
综上,当
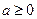 时,函数
时,函数 递增区间是
递增区间是
当
 时,函数
时,函数 递增区间是
递增区间是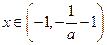 ,递减区间是
,递减区间是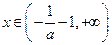 ……13分
……13分
练习册系列答案
相关题目
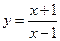 在点
在点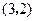 处的切线与直线
处的切线与直线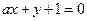 垂直,则
垂直,则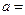 ( )
( )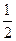
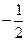
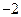
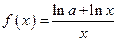 在
在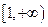 上为减函数,则实数
上为减函数,则实数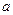 的取值范围是( )
的取值范围是( )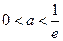
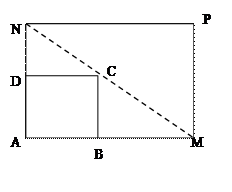 (Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.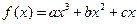 的极小值为
的极小值为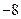 ,其导函数
,其导函数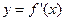 的图像经过点
的图像经过点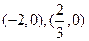 ,如图所示,
,如图所示,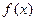 的解析式;
的解析式;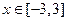 都有
都有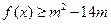 恒成立,
恒成立,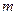 的取值范围。
的取值范围。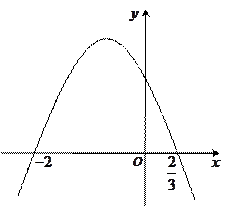
 km处的海岸渔站中,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸可以使抵达渔站的时间最省?
km处的海岸渔站中,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸可以使抵达渔站的时间最省? x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.
x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.
 ,f2(x)=x+2,
,f2(x)=x+2, ,试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积;
,试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积; ],求b的值.
],求b的值.