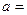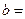题目内容
设三次函数h(x)=px3+qx2+rx+s满足下列条件:h(1)="1,h(-1)=" -1,在区间(-1,1)上分别取得极大值1和极小值-1,对应的极点分别为a,b。
(1)证明:a+b=0
(2)求h(x)的表达式
(3)已知三次函数f(x)=ax3+bx2+cx+d在(-1,1)上满足-1<f(x)<1。证明当|x|>1时,有|f(x)|<|h(x)|
(1)证明:a+b=0
(2)求h(x)的表达式
(3)已知三次函数f(x)=ax3+bx2+cx+d在(-1,1)上满足-1<f(x)<1。证明当|x|>1时,有|f(x)|<|h(x)|
(1)见解析(2)h(x)=4x3-3x(3)见解析
(1)解:由f(1)=1,f(-1)=-1得q+s="0,r+p=1"
h(x)=px3-sx2+(1-p)x+s
h’(x)=3px2-2sx+1-p
因为(-1,1)内有两极值且f(1)=1,所以有p>0
 =0(*)
=0(*)
又由韦达定理得 ,即
,即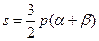 代入(*)中得
代入(*)中得
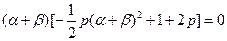
因为p>0,a+bÎ(-2,2),所以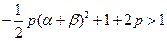
所以有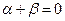
(2)解:由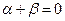 得s=0,q="0"
得s=0,q="0"
所以h(x)=px3+(1-p)x,又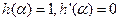
消去p得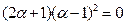 所以有
所以有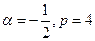
所以有h(x)=4x3-3x
(3)解:因为|x|<1时|f(x)|<1,所以有|f(1)|£1,|f(-1)|£1
令F(x)=h(x)+f(x),G(x)=h(x)-f(x)
则有F(1)=1+f(1)³0,F(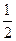 )=-1+f(
)=-1+f(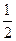 )<0,F(
)<0,F(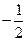 )=1+f(-
)=1+f(-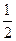 )>0,F(-1)=-1+f(-1)£0
)>0,F(-1)=-1+f(-1)£0
所以有F(x)在(-1,1)内有极大值和极小值,当x>1时,F(x)>0,当x<-1时,F(x)<0
同理有:G(1)=1-f(1)³0, G(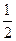 )=-1-f(
)=-1-f(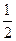 )<0, G(
)<0, G(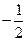 )=1-f(-
)=1-f(-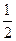 )>0,
)>0,
G(-1)=-1-f(-1)£0
所以有G(x)在(-1,1)内有极大值和极小值,当x>1时,G(x)>0,当x<-1时,G(x)<0
所以当|x|>1时,有F(x)G(x)>0即h2(x)>f2(x)即|h(x)|>|f(x)
h(x)=px3-sx2+(1-p)x+s
h’(x)=3px2-2sx+1-p
因为(-1,1)内有两极值且f(1)=1,所以有p>0
 =0(*)
=0(*)又由韦达定理得
 ,即
,即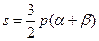 代入(*)中得
代入(*)中得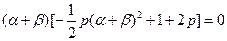
因为p>0,a+bÎ(-2,2),所以
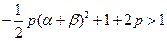
所以有
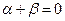
(2)解:由
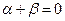 得s=0,q="0"
得s=0,q="0" 所以h(x)=px3+(1-p)x,又
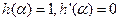
消去p得
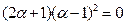 所以有
所以有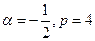
所以有h(x)=4x3-3x
(3)解:因为|x|<1时|f(x)|<1,所以有|f(1)|£1,|f(-1)|£1
令F(x)=h(x)+f(x),G(x)=h(x)-f(x)
则有F(1)=1+f(1)³0,F(
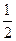 )=-1+f(
)=-1+f(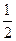 )<0,F(
)<0,F(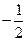 )=1+f(-
)=1+f(-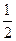 )>0,F(-1)=-1+f(-1)£0
)>0,F(-1)=-1+f(-1)£0所以有F(x)在(-1,1)内有极大值和极小值,当x>1时,F(x)>0,当x<-1时,F(x)<0
同理有:G(1)=1-f(1)³0, G(
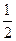 )=-1-f(
)=-1-f(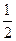 )<0, G(
)<0, G(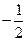 )=1-f(-
)=1-f(-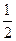 )>0,
)>0,G(-1)=-1-f(-1)£0
所以有G(x)在(-1,1)内有极大值和极小值,当x>1时,G(x)>0,当x<-1时,G(x)<0
所以当|x|>1时,有F(x)G(x)>0即h2(x)>f2(x)即|h(x)|>|f(x)

练习册系列答案
相关题目
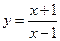 在点
在点 处的切线与直线
处的切线与直线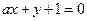 垂直,则
垂直,则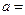 ( )
( )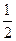
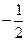
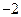
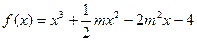 (m为常数,且m>0)有极大值
(m为常数,且m>0)有极大值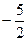 ,
,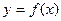 的斜率为2的切线方程.
的斜率为2的切线方程.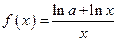 在
在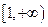 上为减函数,则实数
上为减函数,则实数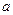 的取值范围是( )
的取值范围是( )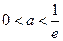
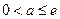
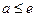
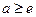
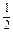 x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.
x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.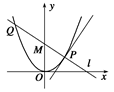
 。
。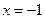 处的切线方程;
处的切线方程;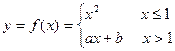 在
在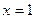 处可导,则
处可导,则