题目内容
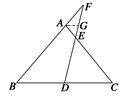
(12分)已知:如图所示,在△ABC中,D是BC的中点,F是BA延长线上的点,FD与AC交于点E.
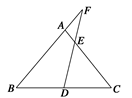
求证:AE·FB=EC·FA.

求证:AE·FB=EC·FA.
见解析。
本小题可以先采用分析法进行推理,然后再利用综合法进行证明.
要证:AE·FB=EC·FA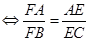 ,然后可考虑过A作AG//DC交FD于G点.问题进一步转化为
,然后可考虑过A作AG//DC交FD于G点.问题进一步转化为
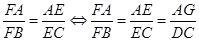 ,因为BD=CD,所以
,因为BD=CD,所以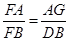 即可.到此问题得证.
即可.到此问题得证.
过A作AG∥BC,交DF于G点.
∵AG∥BD,∴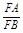 =
=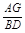 .
.
又∵BD=DC,∴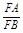 =
=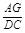 .
.
∵AG∥CD,∴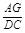 =
=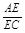 .
.
∴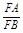 =
=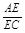 .∴AE·FB=EC·FA.
.∴AE·FB=EC·FA.
要证:AE·FB=EC·FA
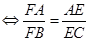 ,然后可考虑过A作AG//DC交FD于G点.问题进一步转化为
,然后可考虑过A作AG//DC交FD于G点.问题进一步转化为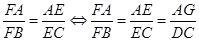 ,因为BD=CD,所以
,因为BD=CD,所以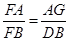 即可.到此问题得证.
即可.到此问题得证.过A作AG∥BC,交DF于G点.

∵AG∥BD,∴
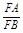 =
=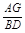 .
.又∵BD=DC,∴
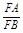 =
=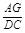 .
.∵AG∥CD,∴
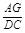 =
=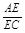 .
.∴
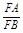 =
=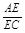 .∴AE·FB=EC·FA.
.∴AE·FB=EC·FA.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
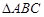 内接于⊙
内接于⊙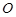 ,
, 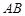 是⊙
是⊙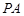 是过点
是过点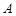 的直线, 且
的直线, 且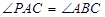 .
.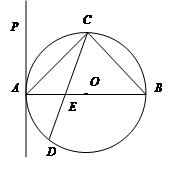
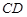 交
交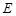 ,
, 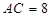 ,
, 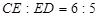 ,
, 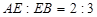 , 求
, 求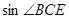 .
.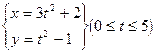
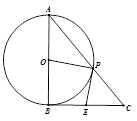
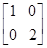 ,N=
,N=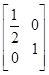 ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.
,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.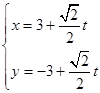 (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
(t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.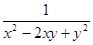 ≥2y+3.
≥2y+3.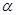 ,且DM交AC于F,EM交BD于G。
,且DM交AC于F,EM交BD于G。 ,AF=3,求FG长。
,AF=3,求FG长。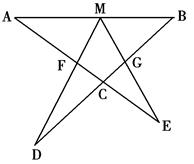
 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。