题目内容
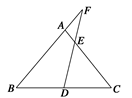
如图设M为线段AB中点,AE与BD交于点C ∠DME=∠A=∠B=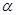 ,且DM交AC于F,EM交BD于G。
,且DM交AC于F,EM交BD于G。
(1)写出图中三对相似三角形,并对其中一对作出证明;
(2)连结FG,设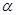 =45°,AB=4
=45°,AB=4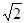 ,AF=3,求FG长。
,AF=3,求FG长。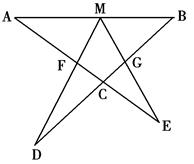
 ,且DM交AC于F,EM交BD于G。
,且DM交AC于F,EM交BD于G。(1)写出图中三对相似三角形,并对其中一对作出证明;
(2)连结FG,设
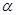 =45°,AB=4
=45°,AB=4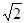 ,AF=3,求FG长。
,AF=3,求FG长。
△AME∽△MFE,△BMD∽△MGD, △AMF∽△BGM …………3分
∵∠AMD=∠B+∠D ∠BGM=∠DMG+∠D
又∠B=∠A=∠DME=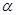
∴∠AMF=∠BGM ∴△AMF∽△BGM …………5分
(II)由(1)△AMF∽△BGM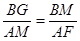
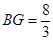
∠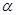 =45° ∴△ABC为等腰直角三角形
=45° ∴△ABC为等腰直角三角形
AB=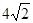 AC=BC=4, CF=AC-AF=1 CG=4-
AC=BC=4, CF=AC-AF=1 CG=4-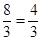
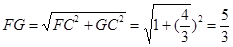
∵∠AMD=∠B+∠D ∠BGM=∠DMG+∠D
又∠B=∠A=∠DME=
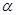
∴∠AMF=∠BGM ∴△AMF∽△BGM …………5分
(II)由(1)△AMF∽△BGM
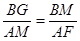
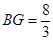
∠
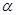 =45° ∴△ABC为等腰直角三角形
=45° ∴△ABC为等腰直角三角形AB=
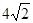 AC=BC=4, CF=AC-AF=1 CG=4-
AC=BC=4, CF=AC-AF=1 CG=4-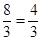
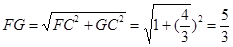
略

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
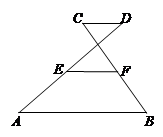
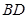 是
是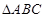 边
边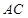 的中线,
的中线,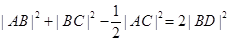 .
.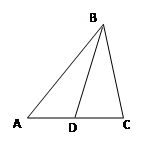
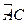 上的点(不与点A , C重合),延长BD至E。
上的点(不与点A , C重合),延长BD至E。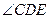 ;
;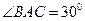 ,△ABC中BC边上的高为
,△ABC中BC边上的高为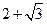 ,
,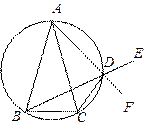
 ⊙O于点P,交BC的延长线于点D,
⊙O于点P,交BC的延长线于点D,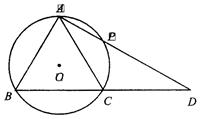
 BO,ON=
BO,ON= OC.设向量
OC.设向量 =a,
=a, =b
=b

 ;w
;w



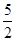

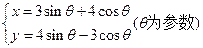 ,则此圆的半径为_______________。
,则此圆的半径为_______________。