题目内容
直线
(t为参数)被圆(x-3)2+(y+1)2=25所截得的弦长为.
|
∵直线
(t为参数),
∴直线的一般式方程为x+y+1=0,
∵圆(x-3)2+(y+1)2=25,则圆心为(3,-1),半径r=5,
∴圆心(3,-1)到直线x+y+1=0的距离d=
=
,
设弦长为l,则根据勾股定理可得,d2+(
l)2=r2,
故(
)2+(
l)2=25,解得l=
,
故直线被圆所截得的弦长为
.
|
∴直线的一般式方程为x+y+1=0,
∵圆(x-3)2+(y+1)2=25,则圆心为(3,-1),半径r=5,
∴圆心(3,-1)到直线x+y+1=0的距离d=
| |3-1+1| | ||
|
3
| ||
| 2 |
设弦长为l,则根据勾股定理可得,d2+(
| 1 |
| 2 |
故(
3
| ||
| 2 |
| 1 |
| 2 |
| 82 |
故直线被圆所截得的弦长为
| 82 |

练习册系列答案
相关题目
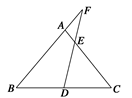
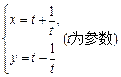 相交于A、B两点.求线段AB的长.
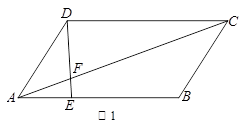
相交于A、B两点.求线段AB的长.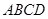 中,点
中,点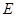 在
在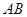 上且
上且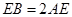 ,
,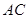 与
与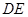 交于点
交于点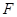 ,则
,则 .
.
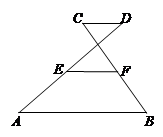
 ⊙O于点P,交BC的延长线于点D,
⊙O于点P,交BC的延长线于点D,
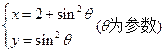 化为普通方程为( )
化为普通方程为( )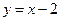
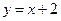
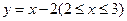
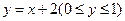
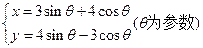 ,则此圆的半径为_______________。
,则此圆的半径为_______________。