Question

【题目】设函数

（1）若不等式对恒成立，求的值；

（2）若在内有两个极值点，求负数的取值范围；

（3）已知，若对任意实数，总存在实数，使得成立，求正实数的取值集合．

Answer 1

【答案】见解析

【解析】解（1）若 ，则当时，，不合题意；

若 ，则当时，，不合题意；

若 ，则当时，，当时，，当时，，满足题意，因此的值为 ……………4分

（2）,

令，则

所以在上单调递减，在上单调递增，因此………6分

(i)当时， 在内至多有一个极值点；

(ii) 当时，由于 所以 ，而，因此在上无零点，在上有且仅有一个零点，从而在上有且仅有一个零点，在内有且仅有一个极值点；………………………8分

(iii)当时，因此在上有且仅有一个零点，在上有且仅有一个零点，从而在上有且仅有两个零点，在内有且仅有两个极值点；

综上负数的取值范围为………………………10分

（3）因为对任意实数，总存在实数，使得成立，所以函数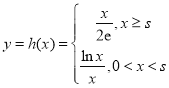的值域为．

在上是增函数，其值域为 ………………11分

对于函数，当时，，

当时，，函数在上为单调减函数，

当时，，函数在上为单调增函数．

若，则函数在上是增函数，在上是减函数，其值域为，

又，不符合题意，舍去；………………13分

若，则函数在上是增函数，值域为，

由题意得，即 ①

记则

当时，，在上为单调减函数．

当时，，在上为单调增函数，

所以，当时，有最小值，

从而恒成立(当且仅当时，) ②………………15分

由①②得，，所以

综上所述，正实数的取值集合为．………………16分

【命题意图】本题考查利用导数及零点存在定理研究极值点，利用单调性研究不等式恒成立等基础知识，意在考查学生转化与化归能力、综合分析问题解决问题的能力以及运算求解能力．