题目内容
10.已知函数f(x)=2ax+$\frac{1}{x}$(a∈R).(1)当$a=\frac{1}{2}$时,试判断f(x)在(0,1]上的单调性并用定义证明你的结论;
(2)对于任意的x∈(0,1],使得f(x)≥6恒成立,求实数a的取值范围.
分析 (1)a代入可得$f(x)=x+\frac{1}{x}$,利用定义法证明函数单调性,判断f(x1)-f(x2)的正负;
(2)整理不等式可得2ax+$\frac{1}{x}$≥6 恒成立,即$2a≥6(\frac{1}{x})-{(\frac{1}{x})^2}$,只需求出右式的最大值,利用二次函数性质可求.
解答 解:(1)∵$a=\frac{1}{2}$
∴$f(x)=x+\frac{1}{x}$
f(x)在(0,1]上的单调递减 …(2分)
证明:取任意的x1,x2,且0<x1<x2≤1
$\begin{array}{l}f({x_1})-f({x_2})={x_1}+\frac{1}{x_1}-{x_2}-\frac{1}{x_2}={x_1}-{x_2}+\frac{{{x_2}-{x_1}}}{{{x_1}{x_2}}}\\ \begin{array}{l}{\;}&{\;}&{\;}&{\;}&{=({x_1}-{x_2})\frac{{({x_1}{x_2}-1)}}{{{x_1}{x_2}}}}\end{array}\begin{array}{l}{\;}&{(*)}\end{array}\end{array}$
∵0<x1<x2≤1,
∴x1-x2<0,0<x1x2<1
得 f(x1)-f(x2)>0
所以f(x)在(0,1]上的单调递减 …(8分)
(2)由f(x)≥6在(0,1]上恒成立,
∴2ax+$\frac{1}{x}$≥6 恒成立
即$2a≥6(\frac{1}{x})-{(\frac{1}{x})^2}$$(\frac{1}{x})∈[1,+∞)$$⇒{(6(\frac{1}{x})-{(\frac{1}{x})^2})_{max}}=9$$⇒2a≥9\begin{array}{l}{\;}{\;}{即a≥\frac{9}{2}}\end{array}$…(14分)
点评 考查了利用定义法证明函数的单调性和恒成立问题的转换.

| A. | 一定在直线y=qx-a上 | B. | 一定在直线y=ax+q上 | ||
| C. | 一定在直线y=ax-q上 | D. | 一定在直线y=qx+a上 |
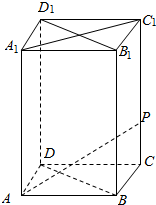 如图,在底面边长为1,侧棱长为2的正四棱柱ABCDA1B1C1D1中,P是侧棱CC1上的一点,CP=1,求异面直线AP与BD1所成角的余弦.
如图,在底面边长为1,侧棱长为2的正四棱柱ABCDA1B1C1D1中,P是侧棱CC1上的一点,CP=1,求异面直线AP与BD1所成角的余弦.