题目内容
1.在△ABC中,角A,B,C的对边分别为a,b,c,且a2-(b-c)2=(2-$\sqrt{3}$)bc,sinAsinB=cos2$\frac{C}{2}$,(1)求角B的大小;
(2)若等差数列{an}的公差不为零,且a1cos2B=1,且a2、a4、a8成等比数列,求{$\frac{4}{{a}_{n}{a}_{n+1}}$}的前n项和Sn.
分析 (1)由a2-(b-c)2=(2-$\sqrt{3}$)bc,化简后利用余弦定理可求cosA,又0<A<π,解得A,由sinAsinB=cos2$\frac{C}{2}$,可得sinB=1+cosC,又C为钝角,解得cos(C+$\frac{π}{3}$)=-1,从而可求C,进而求得B的值.
(2)设{an}的公差为d,由已知得a1=2,且(a1+3d)2=(a1+d)(a1+7d).解得d=2.an=2n.由$\frac{4}{{a}_{n}{a}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.即可用裂项法求和.
解答 解:(1)由a2-(b-c)2=(2-$\sqrt{3}$)bc,可得:a${\;}^{2}-{b}^{2}-{c}^{2}=-\sqrt{3}bc$,
所以cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\sqrt{3}}{2}$,又0<A<π,
∴A=$\frac{π}{6}$,
由sinAsinB=cos2$\frac{C}{2}$,可得$\frac{1}{2}$sinB=$\frac{1+cosC}{2}$,sinB=1+cosC,
∴cosC<0,则C为钝角.B+C=$\frac{5π}{6}$,则sin($\frac{5π}{6}$-C)=1+cosC,
∴cos(C+$\frac{π}{3}$)=-1,
解得C=$\frac{2π}{3}$,∴B=$\frac{π}{6}$.…(6分)
(2)设{an}的公差为d,由已知得a1=$\frac{1}{cosA}=2$,且a24=a2a8.
∴(a1+3d)2=(a1+d)(a1+7d).
又d≠0,∴d=2.∴an=2n.…(9分)
∴$\frac{4}{{a}_{n}{a}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
∴Sn=(1-$\frac{1}{2}$)+($\frac{1}{2}-\frac{1}{3}$)+…+($\frac{1}{n}-\frac{1}{n+1}$)=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.…(12分)
点评 本题主要考查了余弦定理,三角函数恒等变换的应用,考查了等差数列,等比数列的性质和裂项法求和的方法,属于中档题.

| A. | f(x)=sinx | B. | f(x)=ax+a-x(a>0,a≠1) | ||
| C. | f(x)=ln$\frac{3+x}{3-x}$ | D. | f(x)=ax-a-x,(a>0,a≠1) |
| A. | t1+t2 | B. | t1-t2 | C. | $\frac{1}{{t}_{1+}{t}_{2}}$ | D. | $\frac{1}{{t}_{1-}{t}_{2}}$ |
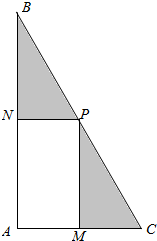 我校为进行“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为$\frac{37k}{{\sqrt{S}}}$元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为$\frac{12k}{{\sqrt{S}}}$元(k为正常数).
我校为进行“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为$\frac{37k}{{\sqrt{S}}}$元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为$\frac{12k}{{\sqrt{S}}}$元(k为正常数).