题目内容
【题目】已知直线l的参数方程是  (t是参数),以坐标原点为极点,x轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆C的极坐标方程为ρ=2
(t是参数),以坐标原点为极点,x轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆C的极坐标方程为ρ=2 ![]() cos(θ+
cos(θ+ ![]() ).
).
(1)求直线l的普通方程与圆C的直角坐标方程;
(2)设圆C与直线l交于A、B两点,若P点的直角坐标为(1,0),求|PA|+|PB|的值.
【答案】
(1)解:∵直线l的参数方程是 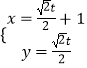 (t是参数),∴x+y=1.
(t是参数),∴x+y=1.
即直线l的普通方程为x+y﹣1=0.
∵ρ=2 ![]() cos(θ+
cos(θ+ ![]() )=2cosθ﹣2sinθ,
)=2cosθ﹣2sinθ,
∴ρ2=2ρcosθ﹣2ρsinθ,
∴圆C的直角坐标方程为x2+y2=2x﹣2y,即x2+y2﹣2x+2y=0
(2)解:将 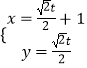 代入x2+y2﹣2x+2y=0得t2﹣
代入x2+y2﹣2x+2y=0得t2﹣ ![]() t﹣1=0,
t﹣1=0,
∴t1+t2= ![]() ,t1t2=﹣1.
,t1t2=﹣1.
∴|PA|+|PB|=|t1﹣t2|= ![]() =
= ![]()
【解析】(1)将参数方程两式相加消去参数t得到直线l的普通方程,将极坐标方程展开两边同乘ρ,根据极坐标与直角坐标的对应关系得到直角坐标方程;(2)将直线l的参数方程代入曲线C的直角坐标方程,利用根与系数的关系和参数的几何意义求出距离.
【考点精析】本题主要考查了直线的参数方程的相关知识点,需要掌握经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为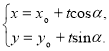 (
(![]() 为参数)才能正确解答此题.
为参数)才能正确解答此题.

【题目】如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.求:

(1) AD边所在直线的方程;
(2) DC边所在直线的方程.
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(1)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(2)商店记录了50天该商品的日需求量(单位:件),整理得表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间[400,550]”为事件A,求P(A)的估计值.