Question

【题目】如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，E是BC的中点，F是棱CD上的动点，G为C1D1的中点，H为A1G的中点．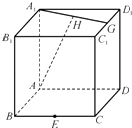

（1）当点F与点D重合时，求证：EF⊥AH；
（2）设二面角C1﹣EF﹣C的大小为θ，试确定点F的位置，使得sin θ= ．

Answer 1

【答案】
（1）证明：以点A为坐标原点，建立如图（2）所示的空间直角坐标系，

则A1（0，0，1），C1（1，1，1），D（0，1，0），E ，

G ，H ，

设F（x，1，0）（0≤x≤1），当点F与点D重合时，易知F（0，1，0），

= ， = ，

∴ =0，∴EF⊥AH．

（2）解：易知 = ， = ，且x≠1．

设 =（a，b，c）是平面C1EF的法向量，则 ，∴ ，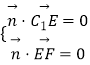

令c=1，则平面C1EF的一个法向量 = ．

又 =（0，0，1）是平面EFC的一个法向量，

∴cos＜ ， ＞= = ，

∵sin θ= ，θ为锐角，∴cosθ= ．

∴ = ，解得x= 或x= （舍去）．

故当F是CD的中点时，sin θ= ．

【解析】（1）以点A为坐标原点，建立如图（2）所示的空间直角坐标系，设F（x，1，0）（0≤x≤1），当点F与点D重合时，易知F（0，1，0），只要证明 =0，即可得出EF⊥AH．（2）sin θ= ，θ为锐角，可得cosθ= ．设 =（a，b，c）是平面C1EF的法向量，则 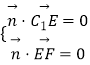，可得平面C1EF的一个法向量 = ．又 =（0，0，1）是平面EFC的一个法向量，利用cos＜ ， ＞= ，解出即可得出．
【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本，需要知道相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．