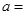题目内容
一块形状为直角三角形的铁皮,直角边长分别为40cm和60cm,现将它剪成一个矩形,并以此三角形的直角为矩形的一个角,问怎样剪才能使剩下的残料最少?
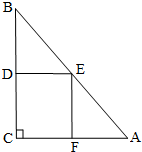

如图所示.设AC=40,BC=60.
则直线AB的方程为
+
=1.
设E(x,y),则
+
=1.(0<x<40,0<y<60).
∴1≥2
,化为xy≤600,当且仅当
=
=
,即x=20,y=30时取等号.
∴S矩形CDEF=xy≤600.
∵△ABC的面积S=
×40×60=1200.是固定的,
∴当使得DE=20,EF=30,剪下矩形CDEF的面积最大时,才能使剩下的残料最少.
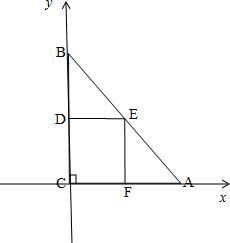
则直线AB的方程为
| x |
| 40 |
| y |
| 60 |
设E(x,y),则
| x |
| 40 |
| y |
| 60 |
∴1≥2
|
| x |
| 40 |
| y |
| 60 |
| 1 |
| 2 |
∴S矩形CDEF=xy≤600.
∵△ABC的面积S=
| 1 |
| 2 |
∴当使得DE=20,EF=30,剪下矩形CDEF的面积最大时,才能使剩下的残料最少.


练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
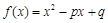 ,其中
,其中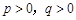 .
.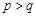 时,证明
时,证明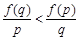 ;
;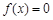 在区间
在区间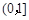 ,
,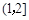 内各有一个根,求
内各有一个根,求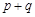 的取值范围;
的取值范围;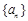 的首项
的首项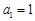 ,前
,前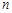 项和
项和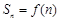 ,
,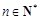 ,求
,求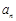 ,并判断
,并判断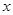 ,
,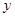 满足约束条件
满足约束条件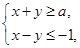 且
且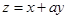 的最小值为7,则
的最小值为7,则