题目内容
已知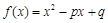 ,其中
,其中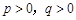 .
.
(1)当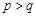 时,证明
时,证明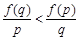 ;
;
(2)若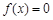 在区间
在区间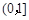 ,
,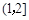 内各有一个根,求
内各有一个根,求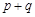 的取值范围;
的取值范围;
(3)设数列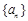 的首项
的首项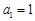 ,前
,前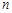 项和
项和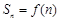 ,
,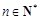 ,求
,求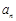 ,并判断
,并判断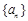 是否为等差数列?
是否为等差数列?
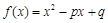 ,其中
,其中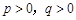 .
.(1)当
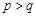 时,证明
时,证明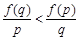 ;
;(2)若
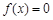 在区间
在区间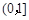 ,
,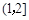 内各有一个根,求
内各有一个根,求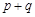 的取值范围;
的取值范围;(3)设数列
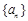 的首项
的首项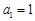 ,前
,前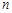 项和
项和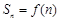 ,
,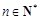 ,求
,求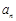 ,并判断
,并判断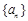 是否为等差数列?
是否为等差数列? (1)详见解析;(2) ;(3)
;(3)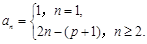 ,
,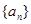 不是等差数列.
不是等差数列.
 ;(3)
;(3)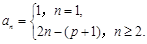 ,
,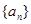 不是等差数列.
不是等差数列.试题分析:(1)根据条件中
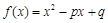 ,可得
,可得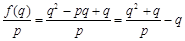 ,
,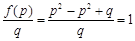 ,从而考虑采用作差法来比较两者的大小:
,从而考虑采用作差法来比较两者的大小: ,再由条件中
,再由条件中 可知
可知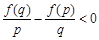 ,即
,即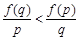 ;(2)可将条件
;(2)可将条件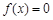 在区间
在区间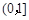 ,
,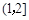 内各有一个根等价转化为二次函数
内各有一个根等价转化为二次函数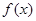 在区间
在区间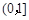 ,
,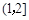 上各有一个零点,因此利用数形结合的思想可知,
上各有一个零点,因此利用数形结合的思想可知,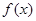 需满足:
需满足: ,则问题等价于在线性约束条件
,则问题等价于在线性约束条件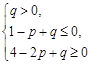 ,求线性目标函数
,求线性目标函数 的取值范围,将线性约束条件表示的可行域画出,即可得
的取值范围,将线性约束条件表示的可行域画出,即可得 ;(3)由题意可知
;(3)由题意可知 ,考虑到当
,考虑到当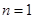 时,
时,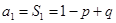 ,当
,当 ,
,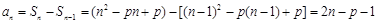 ,因此数列
,因此数列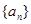 的通项公式为
的通项公式为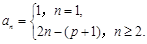 ,从而可得
,从而可得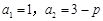 ,
, (
( ),由p>0,q>0可知
),由p>0,q>0可知 ,故
,故 不是等差数列.
不是等差数列.试题解析:(1)
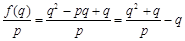 ,
,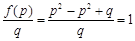 , 1分
, 1分∴
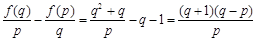 , 3分
, 3分∵
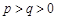 ,∴
,∴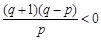 ,即
,即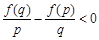 ,
,∴
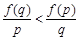 ; 4分
; 4分(2)
 抛物线的图像开口向上,且
抛物线的图像开口向上,且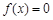 在区间
在区间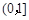 ,
,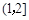 内各有一个根,
内各有一个根,∴
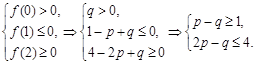 6分
6分∴点
 (
(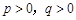 )组成的可行域如图所示, 8分
)组成的可行域如图所示, 8分由线性规划知识可知,
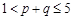 ,即
,即 . 9分
. 9分
(3)由题意可知,
 ,
,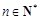 .
.当
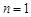 时,
时,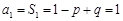 ,∴
,∴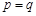 . 10分
. 10分当
 时,
时,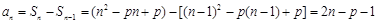 ,
, ∴
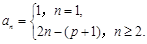 12分
12分∵
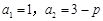 ,
, (
( ),
),∵
 ,
, 从而可知,
从而可知, ,∴
,∴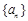 不是等差数列. 14分
不是等差数列. 14分
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
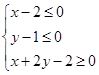 表示的平面区域上运动,则x-y的取值范围是( ).
表示的平面区域上运动,则x-y的取值范围是( ).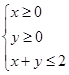 ,则z=4x+y的最大值为( )
,则z=4x+y的最大值为( )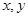 满足约束条件
满足约束条件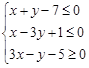 ,则
,则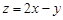 的最大值为( )
的最大值为( )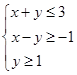 ,则目标函数z=2x+y的最大值为 .
,则目标函数z=2x+y的最大值为 .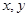 满足约束条件
满足约束条件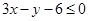 ,
,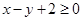 ,
,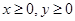 ,若目标函数
,若目标函数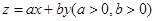 的最大值为12,则
的最大值为12,则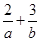 的最小值为( )
的最小值为( )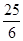
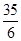
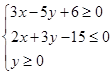 ,当且仅当x=y=3时,z=ax-y取得最小值,则实数a的取值范围是________.
,当且仅当x=y=3时,z=ax-y取得最小值,则实数a的取值范围是________.