题目内容
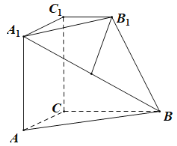
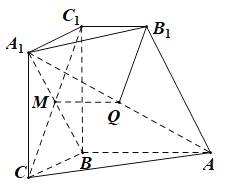
【题目】如图，在几何体
中，平面
⊥底面
，四边形是正方形，
，
是
的中点，且
，
（1）证明：
//平面；
（2）求直线
与平面
所成角的正弦值.
【答案】（1）证明见解析（2）
【解析】
（1）连接
，
交于
点，连接
，证明四边形
是平行四边形得到答案.
（2）过点
作面
与面
的交线
，交直线
于
，证明
即
与面所成的角，计算得到答案.
（1）证明：如图1所示，连接，交于点，连接.
因为四边形
是正方形，所以是的中点，
又已知
是
的中点，所以
，
又因为
且
，所以
，即四边形是平行四边形，
所以
，因此
平面.
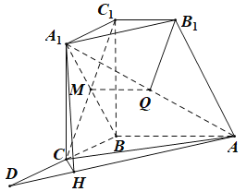
（2）如图2所示，过点作面与面的交线，交直线于.
过
作线的垂线
，垂足为
.
再过作线的垂线
，垂足为
.
因为
，
，所以
面
，
所以
，又因为
，
所以⊥面，所以即与面所成的角，
因为
面，所以
，
且为
的中点，如图2所示，
为边上的高，
，
，
因为
，所以
，所以
，
因为
，所以
，
，
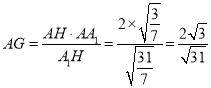所以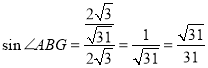
.
练习册系列答案
相关题目
【题目】某家庭记录了未使用节水龙头50天的日用水量数据（单位：m3）和使用了节水龙头50天的日用水量数据，得到频数分布表如下：
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
（1）在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图：
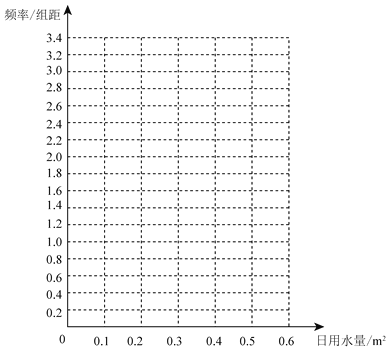
（2）估计该家庭使用节水龙头后，日用水量小于0.35 m3的概率；
（3）估计该家庭使用节水龙头后，一年能节省多少水？（一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表．）
