题目内容
4.在数列{an}中,已知an=3an-1+1(n≥2),a3=13(1)求a1的值;
(2)求数列{an}的通项公式;
(3)求证:对一切正整数n,都有$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$<$\frac{3}{2}$.
分析 (1)直接代入计算即可;
(2)对an=3an-1+1(n≥2)变形可得${a}_{n}+\frac{1}{2}=3({a}_{n-1}+\frac{1}{2})$,进而可得结论;
(3)由(2)及放缩法可得$\frac{1}{{a}_{n}}$<$\frac{1}{{2}^{n}}$(n≥2),利用等比数列的求和公式计算即可.
解答 (1)解:∵an=3an-1+1(n≥2),
∴a2=3a1+1,
∴a3=3a2+1=9a1+4=13,
解得a1=1;
(2)解:∵an=3an-1+1(n≥2),
∴${a}_{n}+\frac{1}{2}=3({a}_{n-1}+\frac{1}{2})$,
即数列{${a}_{n}+\frac{1}{2}$}是以$\frac{3}{2}$为首项、公比为3的等比数列,
∴${a}_{n}+\frac{1}{2}$=$\frac{1}{2}•{3}^{n}$,
∴an=$\frac{1}{2}({3}^{n}-1)$;
(3)证明:∵an=$\frac{1}{2}({3}^{n}-1)$,∴$\frac{1}{{a}_{n}}$=$\frac{2}{{3}^{n}-1}$,
∵$\frac{2}{{3}^{n}-1}$<$\frac{1}{{2}^{n}}$(n≥2),
∴对一切正整数n,都有:
$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$≤1+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$
=1+$\frac{1}{4}•\frac{1-(\frac{1}{2})^{n-1}}{1-\frac{1}{2}}$
<1+$\frac{1}{2}$-$(\frac{1}{2})^{n}$
<$\frac{3}{2}$.
点评 本题考查求数列的通项、前n项和,考查放缩法,对表达式的灵活变形是解决本题的关键,属于中档题.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | a12 | B. | a13 | C. | a12或a13 | D. | 不存在 |
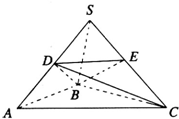 如图,在三棱锥S-ABC中,SB⊥底面ABC,且SB=AB=2,BC=$\sqrt{6},∠ABC=\frac{π}{2}$,D、E分别是SA、SC的中点.
如图,在三棱锥S-ABC中,SB⊥底面ABC,且SB=AB=2,BC=$\sqrt{6},∠ABC=\frac{π}{2}$,D、E分别是SA、SC的中点.