题目内容
12.已知函数f(x)=ax2+8x+b,g(x)=(a-1)x2+2(4-a)x.(1)若h(x)=f(x)-g(x)在区间[1,2]内有两个不同的零点,求4a+5b的取值范围;
(2)若b=3,对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5都成立,试求l(a)的解析式,并求l(a)的最大值.
分析 (1)由题意可得h(x)=0在区间[1,2]内有两个不同的实数解,结合判别式大于0,对称轴和端点的函数值,得到不等式组,画出平面区域,运用平移法,即可得到所求范围;
(2)运用配方和分类讨论的思想方法,分-8<a<0时,a≤-8时,结合二次方程的求根公式,二次函数的最值,即可得到l(a)的解析式和最大值.
解答 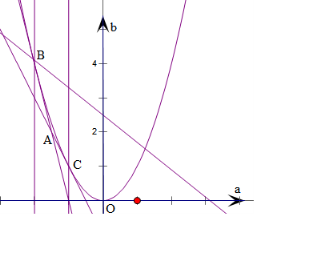 解:(1)h(x)=f(x)-g(x)
解:(1)h(x)=f(x)-g(x)
=ax2+8x+b-(a-1)x2-2(4-a)x
=x2+2ax+b,由题意可得h(x)=0在区间[1,2]内有两个不同的实数解,
则有$\left\{\begin{array}{l}{{a}^{2}-b>0}\\{-2<a<-1}\\{1+2a+b>0}\\{4+4a+b>0}\end{array}\right.$,在直角坐标系中画出它们表示的平面区域,(由图中A,B,C构成的区域不包括边界),
将4a+5b=0平移,当经过点B(-2,4)时,4a+5b=12,
经过点C(-1,1)时,4a+5b=1,
则有4a+5b的取值范围是(1,12);
(2)f(x)=a(x+$\frac{4}{a}$)2+3-$\frac{16}{a}$.
(1)当3-$\frac{16}{a}$>5,即-8<a<0时,
l(a)是方程ax2+8x+3=5的较小根,故l(a)=$\frac{-8+\sqrt{64+8a}}{2a}$.
(2)当3-$\frac{16}{a}$≤5,即a≤-8时,
l(a)是方程ax2+8x+3=-5的较大根,故l(a)=$\frac{-8-\sqrt{64-32a}}{2a}$.
综合以上,l(a)=$\left\{\begin{array}{l}{\frac{-8-\sqrt{64-32a}}{2a},a≤-8}\\{\frac{-8+\sqrt{64+8a}}{2a},-8<a<0}\end{array}\right.$.
当a≤-8时,l(a)=$\frac{-8+\sqrt{64-32a}}{2a}$=$\frac{4}{\sqrt{4-2a}-2}$≤$\frac{4}{\sqrt{20}-2}$=$\frac{1+\sqrt{5}}{2}$;
当-8<a<0时,l(a)=$\frac{-8+\sqrt{64+8a}}{2a}$=$\frac{2}{\sqrt{16+2a}+4}$<$\frac{2}{4}$<$\frac{1+\sqrt{5}}{2}$.
所以a=-8时,l(a)取得最大值$\frac{1+\sqrt{5}}{2}$.
点评 本题考查二次方程实根的分布,以及二次函数的最值的求法,同时考查不等式组表示的平面区域和最值的求法,运用分类讨论的思想方法是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 120x3 | B. | 160x2 | C. | 120 | D. | 160 |
| A. | f(x1)>f(x2) | B. | f(x1)<f(x2) | ||
| C. | f(x1)=f(x2) | D. | f(x2)与f(x2)的大小无法确定 |
 如图四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,且CD=2,AB=BC=PA=1,PD=$\sqrt{3}$.
如图四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,且CD=2,AB=BC=PA=1,PD=$\sqrt{3}$. 已知顶点在原点的抛物线的焦点与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点F重合,过抛物线准线与x轴交点E作直线l与抛物线相交于两个不同的点M、N
已知顶点在原点的抛物线的焦点与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点F重合,过抛物线准线与x轴交点E作直线l与抛物线相交于两个不同的点M、N