题目内容
10.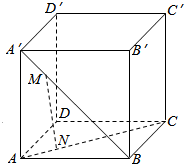 在正方体ABCD-A′B′C′D中,M,N分别是A′B,AC上的点,且A′M=AN,求证:MN∥平面BB′CC′.
在正方体ABCD-A′B′C′D中,M,N分别是A′B,AC上的点,且A′M=AN,求证:MN∥平面BB′CC′.
分析 过点M作MP⊥AB,垂足为P,连接NP,证明平面MNP∥平面B′BCC′,再证明MN∥平面B′BCC′即可.
解答 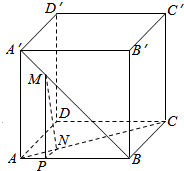 证明:过点M作MP⊥AB,垂足为P,连接NP,如图所示,
证明:过点M作MP⊥AB,垂足为P,连接NP,如图所示,
则MP∥A′A∥B′B;
又MP?平面B′BCC′,B′B?平面B′BCC′,
∴MP∥平面B′BCC′;
A′M:MB=AP:PB,AN:NC=A′M:MB,
∴AN:NC=AP:PB,
∴NP∥CB,
又NP?平面B′BCC′,CB?平面B′BCC′,
∴NP∥平面B′BCC′;
又MP∩NP=P,MP?平面MNP,NP?平面MNP,
∴平面MNP∥平面B′BCC′;
又MN?平面MNP,
∴MN∥平面B′BCC′.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了识图与用图的能力,是基础题目.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
5.若实数x,y满足{x−y≤0x+y−4≤0x≥0,则|3x+y-4|+|x+2y+8|的最小值是( )
| A. | 11 | B. | 12 | C. | 16 | D. | 18 |
2.若→z是z的共轭复数,且满足→z•(1-i)2=4+2i,则z=( )
| A. | -1+2i | B. | -1-2i | C. | 1+2i | D. | 1-2i |