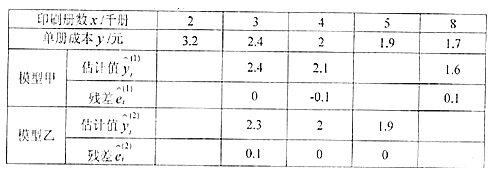
题目内容
【题目】定义：若两个二次曲线的离心率相等，则称这两个二次曲线相似．如图，椭圆C的中心在原点，焦点在x轴上，右顶点为A，以其短轴的两个端点B1 ， B2及其一个焦点为顶点的三角形是边长为6的正三角形，M是C上异于B1 ， B2的一个动点，△MB1B2的重心为G，G点的轨迹记为C1 ．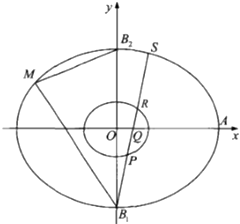 
（1）（i）求C的方程；
（ii）求证：C1与C相似；
（2）过B1点任作一直线，自下至上依次与C1、x轴的正半轴、C交于不同的四个点P，Q，R，S，求 
的取值范围．
【答案】
（1）（i）解：设C的方程： 
+ 
=1（a＞b＞0），则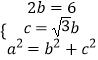 
，
∴a=6，b=3，
∴C的方程： 
=1；
（ii）证明：设G（x，y），M（x0，y）（x0≠0），则x0=3x，y0=3y
把点M（3x，3y）的坐标代入C的方程，得轨迹C1的方程为 
=1（x≠0），
∴轨迹C1也为椭圆（除去（0，﹣1），（0，1）两点），求得a1=2，c1= 
，e1= 
，
∵C的离心率e= ，
∴e1=e，
∴C1与C相似；
（2）解：设直线方程为y=kx﹣3（k＞0），代入C的方程得（1+4k2）x2﹣24kx=0，∴xS= 
，yS= 
，
∴ 
= 
，
代入C1的方程得（1+4k2）x2﹣24kx+32=0，由k＞0，△＞0得k＞ 
，
由韦达定理得xP+xR= ，xPxR= 
，
∴|PR|2=（1+k2）[ 
﹣ 
]．
∵|AQ|=6﹣ 
= 
，
∴ 
= 
令f（k）= （k 
）
则f′（k）= 
＜0
∴f（k）在（ ，+∞）上是减函数，
∴ 
）= 
∴0＜ ＜
【解析】（1）（i）设C的方程： + =1（a＞b＞0），则 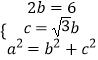，求出a，b，即可求C的方程；（ii）求出轨迹C1 ， 可得离心率相等，即可证明C1与C相似；（2）设直线方程为y=kx﹣3（k＞0），代入椭圆方程，求出相应线段的长，可得 = 构造函数，利用导数确定函数的单调性，即可确定 的取值范围．
