题目内容
设函数f(x)=
.
(Ⅰ)求函数f(x)在区间[-2,2]上的最大值和最小值;
(Ⅱ)设函数f(x)在区间[-4,6]上的最大值为g(a),试求g(a)的表达式.
|
(Ⅰ)求函数f(x)在区间[-2,2]上的最大值和最小值;
(Ⅱ)设函数f(x)在区间[-4,6]上的最大值为g(a),试求g(a)的表达式.
(Ⅰ)在区间[-2,2]上,f(x)=(2-x)(x+4)=-x2-2x+8.
其对称轴为x=-1,且开口向下,如图,
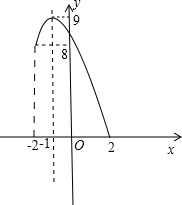
所以f(x)在区间[-2,-1]上单调递增,在区间[-1,2]上单调递减,
所以f(x)在区间[-2,2]上的最大值为f(-1)=-(-1)2-2×(-1)+8=9,
最小值为f(2)=-22-2×2+8=0.
(Ⅱ)当x>2时,f(x)=(2-x)(x-a)=-x2+(a+2)x-2a
函数的对称轴为x=
,且横过定点(2,0).
当a≤2时,f(x)在[-4,-1]上单调递增,在[-1,6]上单调递减,
所以f(x)的最大值为f(-1)=9.
当2<a≤8时,f(x)在[-4,-1]上单调递增,在[-1,2]上单调递减,
在[2,
]单调递增,在[
,6]上单调递减,
此时f(-1)=9,f(
)=(
)2≤9,所以f(x)的最大值为9.
当8<a≤10时,f(x)在[-4,-1]上单调递增,在[-1,2]上单调递减,
在[2,
]单调递增,在[
,6]上单调递减.
此时f(
)=(
)2>f(-1),所以f(x)的最大值为
.
当a>10时,f(x)在[-4,-1]上单调递增,在[-1,2]上单调递减,在[2,6]单调递增,
此时f(6)=4(a-6)>f(-1),所以f(x)的最大值为4(a-6).
综上,g(a)=
其对称轴为x=-1,且开口向下,如图,

所以f(x)在区间[-2,-1]上单调递增,在区间[-1,2]上单调递减,
所以f(x)在区间[-2,2]上的最大值为f(-1)=-(-1)2-2×(-1)+8=9,
最小值为f(2)=-22-2×2+8=0.
(Ⅱ)当x>2时,f(x)=(2-x)(x-a)=-x2+(a+2)x-2a
函数的对称轴为x=
| a+2 |
| 2 |
当a≤2时,f(x)在[-4,-1]上单调递增,在[-1,6]上单调递减,
所以f(x)的最大值为f(-1)=9.
当2<a≤8时,f(x)在[-4,-1]上单调递增,在[-1,2]上单调递减,
在[2,
| a+2 |
| 2 |
| a+2 |
| 2 |
此时f(-1)=9,f(
| a+2 |
| 2 |
| a-2 |
| 2 |
当8<a≤10时,f(x)在[-4,-1]上单调递增,在[-1,2]上单调递减,
在[2,
| a+2 |
| 2 |
| a+2 |
| 2 |
此时f(
| a+2 |
| 2 |
| a-2 |
| 2 |
| (a-2)2 |
| 4 |
当a>10时,f(x)在[-4,-1]上单调递增,在[-1,2]上单调递减,在[2,6]单调递增,
此时f(6)=4(a-6)>f(-1),所以f(x)的最大值为4(a-6).
综上,g(a)=
|

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
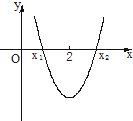

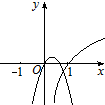


 的值域是( )
的值域是( )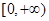



 x2的值域是________.
x2的值域是________.