题目内容
过双曲线 的左焦点F(-c,0)(c >0),作圆:
的左焦点F(-c,0)(c >0),作圆: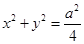 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若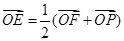 ,则双曲线的离心率为
,则双曲线的离心率为
A.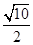 | B. | C. | D. |
A
解析试题分析:设双曲线的另一个焦点为F′。
∵|OF|=c,|OE|=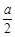 ,∴|EF|=
,∴|EF|=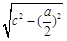 ,
,
∵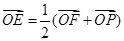 ,∴|PF|=2
,∴|PF|=2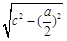 ,|PF'|=a,
,|PF'|=a,
∵|PF|-|PF′|=2a,∴2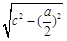 -a=2a,∴e=
-a=2a,∴e=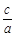 =
=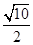 ,选A。
,选A。
考点:本题主要考查双曲线的标准方程及其几何性质,圆的标准方程,平面向量的线性运算。
点评:小综合题,借助于数形结合思想,利用双曲线的定义等,建立e的方程。注意在双曲线中,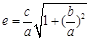 。
。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
设 、
、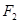 分别是椭圆
分别是椭圆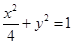 的左、右焦点,
的左、右焦点, 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且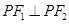 ,则点
,则点 的横坐标为
的横坐标为
A.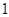 | B.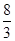 | C.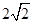 | D.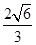 |
双曲线 (a>0,b>0)的离心率是
(a>0,b>0)的离心率是 ,则
,则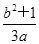 的最小值为 ( )
的最小值为 ( )
A. | B.1 | C.2 | D.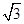 |
曲线 +
+ =1.(m<6) 与
=1.(m<6) 与 +
+ =1.(5<m<9)的( )
=1.(5<m<9)的( )
| A.准线相同 | B.离心率相同 | C.焦点相同 | D.焦距相同 |
若抛物线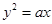 的焦点到准线的距离为4,则此抛物线的焦点坐标为
的焦点到准线的距离为4,则此抛物线的焦点坐标为
A.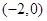 | B.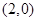 | C.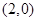 或 或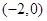 | D.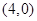 |
设双曲线 的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则|
的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则| |=
|=
A.5 | B.4 | C.3 | D.2 |
 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x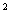 +1 只有一个公共点,则双曲线的离心率为( ).
+1 只有一个公共点,则双曲线的离心率为( ). 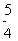
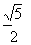
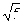
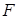 是抛物线
是抛物线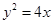 的焦点,准线与
的焦点,准线与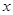 轴的交点为
轴的交点为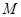 ,点
,点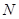 在抛物线上,且
在抛物线上,且 ,则
,则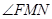 等于( )
等于( )