题目内容
函数f(x)=x3-3x2+1在x=________处取得极小值.
2
f′(x)=3x2-6x=3x(x-2),
当x∈(0,2)时,f′(x)<0;
当x∈(2,+∞)∪(-∞,0)时,f′(x)>0,
∴f(x)在(-∞,0)上是增函数,(0,2)上是减函数,(2,+∞)上是增函数.
所以x=2时,f(x)取得极小值.
当x∈(0,2)时,f′(x)<0;
当x∈(2,+∞)∪(-∞,0)时,f′(x)>0,
∴f(x)在(-∞,0)上是增函数,(0,2)上是减函数,(2,+∞)上是增函数.
所以x=2时,f(x)取得极小值.

练习册系列答案
相关题目
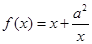 ,
, ,其中
,其中 .
.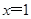 是函数
是函数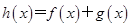 的极值点,求实数
的极值点,求实数 的值;
的值; (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数 (
( ,
, ,
, 且
且 )的图象在
)的图象在 处的切线与
处的切线与 轴平行.
轴平行. 的正、负号;
的正、负号; 在区间
在区间 上有最大值为
上有最大值为 ,求
,求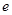 为自然对数的底数,设函数
为自然对数的底数,设函数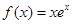 ,则( )
,则( )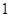 是
是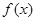 的极小值点
的极小值点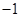 是
是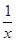 在x>0时有 ( ).
在x>0时有 ( ).
 在
在 时有极值0,则
时有极值0,则 .
.