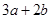题目内容
已知函数f(x)＝x(ln x－ax)有两个极值点，则实数a的取值范围是( )
| A．(－∞，0) | B． |
| C．(0,1) | D．(0，＋∞) |
B
由题知，x>0，f′(x)＝ln x＋1－2ax.由于函数f(x)有两个极值点，则f′(x)＝0有两个不等的正根，显然a≤0时不合题意，必有a>0.令g(x)＝ln x＋1－2ax，g′(x)＝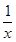
－2a，令g′(x)＝0，得x＝
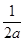，故g(x)在
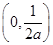上单调递增，在
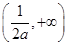上单调递减，所以g(x)在x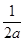＝处取得极大值，即f′
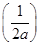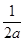＝ln>0，所以0<a<
.
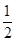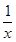－2a，令g′(x)＝0，得x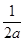＝，故g(x)在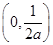上单调递增，在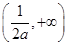上单调递减，所以g(x)在x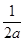＝处取得极大值，即f′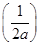＝ln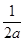>0，所以0<a<.
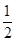练习册系列答案
相关题目
是( ）
在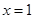
处取极值，则a＝________.
的大致图象如图所示，则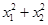
等于（ ）
，则
是函数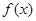
的极值点，因为函数
在
处的导数值
，所以
( )
，其导数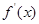
的图象如图所示，则函数
的极大值是（ ）
