题目内容
【题目】已知函数
，对于
，都有
，则实数
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
先分析得到函数f(x)在[0,2]上单调递增，再转化得到0≤
≤1恒成立，分析解答两个不等式恒成立问题即得解.
由题得当
时，
,
所以
，
所以函数f(x)在[0,2]上单调递增，
因为f(1)=4+cosπ=3，
所以
f(1),
所以≤1，
因为≤1且0≤≤2
所以0≤≤1.
当≤1时，
所以
，当x=0时，显然成立.
当0＜x≤2时，
，
所以g(x)在（1,2）单调递增，在（0,1）单调递减，
所以
，所以
.
当≥0时，
，
当x=0时，显然成立.
当0＜x≤2时，
，
令
，
所以k(x)在（0，2）单调递增，所以k(x)>k(0)=0,
所以函数
所以函数h(x)在（0,2]上单调递增，
所以h(x)最大值=h(2)=
.
所以
.
综上得
.
故选：B
练习册系列答案
相关题目
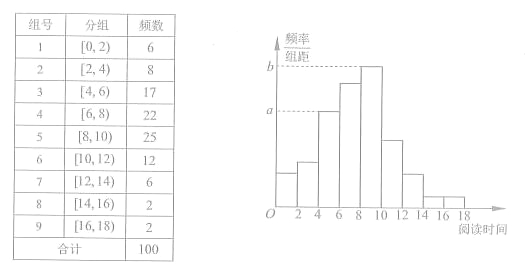
【题目】近年来，某地区积极践行“绿水青山就是金山银山”的绿色发展理念
年年初至
年年初，该地区绿化面积
（单位：平方公里）的数据如下表：
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
绿化面积 |
|
|
|
|
|
|
|
（1）求关于
的线性回归方程；
（2）利用（1）中的回归方程，预测该地区
年年初的绿化面积，并计算
年年初至年年初，该地区绿化面积的年平均增长率约为多少.
（附：回归直线的斜率与截距的最小二乘法估计公式分别为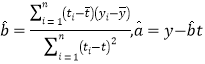
，
）
