题目内容
5.已知数列{an}是等差数列且公差d>0,n∈N*,a1=2,a3为a1和a9的等比中项.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设${b_n}=\frac{2}{{n({{a_n}+2})}}$,求数列{bn}的前n项和Sn.
分析 (1)利用等差数列与等比数列的通项公式即可得出;
(2)利用“裂项求和”即可得出.
解答 解:(Ⅰ)∵a1=2,a3为a1和a9的等比中项,
∴${a_3}^2={a_1}{a_9}$,即(2+2d)2=2(2+8d),
化简得 d2=2d,
∵d>0,解得d=2,
∴an=2+2(n-1)=2n;
(Ⅱ)${b_n}=\frac{2}{{n({{a_n}+2})}}$=$\frac{2}{{n({2n+2})}}$=$\frac{1}{{n({n+1})}}$=$\frac{1}{n}-\frac{1}{n+1}$,
Sn=b1+b2+…+bn=$({1-\frac{1}{2}})+({\frac{1}{2}-\frac{1}{3}})+…+({\frac{1}{n}-\frac{1}{n+1}})$
=$\frac{n}{n+1}$.
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
16.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则( )
| A. | $\overrightarrow{a}$与$\overrightarrow{b}$方向相同 | B. | $\overrightarrow{a}$与$\overrightarrow{b}$方向相反 | C. | $\overrightarrow{a}$与$\overrightarrow{b}$垂直 | D. | 以上都不对 |
17.过椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的右焦点F作两条相互垂直的直线分别交椭圆于A,B,C,D四点,则$\frac{1}{|AB|}+\frac{1}{|CD|}$的值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | 1 | D. | $\frac{7}{12}$ |
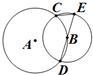 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.