题目内容
【题目】已知在平面直角坐标系![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,
,
(1)求该椭圆的标准方程;
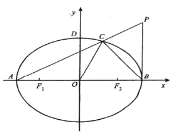
(2)(文)若![]() 是椭圆上的动点,过P作垂直于x轴的垂线,垂足为M,延长MP至N,使得P恰好为MN中点,求点N的轨迹方程;
是椭圆上的动点,过P作垂直于x轴的垂线,垂足为M,延长MP至N,使得P恰好为MN中点,求点N的轨迹方程;
(理)若已知点![]() ,
,![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
【答案】(1)![]() y2=1(2)(文)x2+y2=4.(理)(x
y2=1(2)(文)x2+y2=4.(理)(x![]() )2+4(y
)2+4(y![]() )2=1.
)2=1.
【解析】
(1)由左焦点为F(![]() ),右顶点为D(2,0),得到椭圆的半长轴a,半焦距c,再求得半短轴b,最后由椭圆的焦点在x轴上求得方程.
),右顶点为D(2,0),得到椭圆的半长轴a,半焦距c,再求得半短轴b,最后由椭圆的焦点在x轴上求得方程.
(2)(文)设N(x,y),则M(x,0),利用中点坐标公式可得P(x,![]() ),代入椭圆的标准方程即可得出.
),代入椭圆的标准方程即可得出.
(理)设线段PA的中点为M(x,y),点P的坐标是(x0,y0),由中点坐标公式可知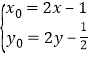 ,将P代入椭圆方程,即可求得线段PA中点M的轨迹方程
,将P代入椭圆方程,即可求得线段PA中点M的轨迹方程
(1)由题意可知:椭圆的焦点在x轴上,设![]() 1(a>b>0),
1(a>b>0),
由椭圆的左焦点为F(![]() ,0),右顶点为D(2,0),即a=2,c
,0),右顶点为D(2,0),即a=2,c![]() ,
,
则b2=a2﹣c2=1,
∴椭圆的标准方程为:![]() y2=1
y2=1
(2)(文)设N(x,y),则M(x,0),利用中点坐标公式可得P(x,![]() ),
),
代入椭圆C1的标准方程为x2+y2=4.
所以N的轨迹方程为x2+y2=4.
(理)设线段PA的中点为M(x,y),点P的坐标是(x0,y0),
由中点坐标公式可知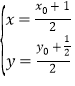 ,整理得:
,整理得: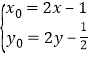 ,
,
由点P在椭圆上,
∴![]() (2y
(2y![]() )2=1,
)2=1,
∴线段PA中点M的轨迹方程是:(x![]() )2+4(y
)2+4(y![]() )2=1.
)2=1.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目