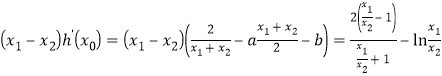Question

【题目】已知函数.

（1）求函数的极值;

（2）当时，证明：;

（3）设函数的图象与直线的两个交点分别为，，的中点的横坐标为，证明：.

Answer 1

【答案】（1）取得极大值，没有极小值（2）见解析（3）见解析

【解析】

（1）利用导数求得函数的单调性，再根据极值的定义，即可求解函数的极值；

（2）由，整理得整理得，设，利用导数求得函数的单调性与最值，即可求解．

（3）不妨设，由（1）和由（2），得，利用单调性，即可作出证明．

（1）由题意，函数，则，

当时，，函数单调递增，

当时，，函数单调递减，

所以当时，取得极大值，没有极小值;

（2）由得

整理得，

设，

则，

所以在上单调递增，

所以，即，

从而有．

（3）证明：不妨设，由（1）知，则，

由（2）知，

由在上单调递减，所以，即，

则，所以.