题目内容
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
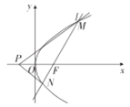
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1)![]()
![]() ;(2)
;(2)![]() .
.
【解析】
(1)设出点P的坐标,向量坐标化得到![]() 的表达式,进而得到最值;(2)
的表达式,进而得到最值;(2)![]() 为锐角即
为锐角即![]() ,设出点AB的坐标,向量坐标化得到点积的表达式为:x1x2+y1y2,联立直线和椭圆方程,由韦达定理得到结果.
,设出点AB的坐标,向量坐标化得到点积的表达式为:x1x2+y1y2,联立直线和椭圆方程,由韦达定理得到结果.
(1)由已知得,F1(-![]() ,0),F2(
,0),F2(![]() ,0),设点P(x,y),
,0),设点P(x,y),
则![]() +y2=1,且-2≤x≤2.
+y2=1,且-2≤x≤2.
所以![]() ·
·![]() =(-
=(-![]() -x,-y)·(
-x,-y)·(![]() -x,-y)=x2-3+y2=x2-3+1-
-x,-y)=x2-3+y2=x2-3+1-![]() =
=![]() x2-2,
x2-2,
当x=0,即P(0,±1)时,(![]() ·
·![]() )min=-2;
)min=-2;
当x=±2,即P(±2,0)时,(![]() ·
·![]() )max=1.
)max=1.
(2)由题意可知,过点M(0,2)的直线l的斜率存在.
设l的方程为y=kx+2,
由 消去y,化简整理得
消去y,化简整理得
(1+4k2)x2+16kx+12=0,Δ=(16k)2-48(1+4k2)>0,解得k2>![]() .
.
设A(x1,y1),B(x2,y2),则x1+x2=-![]() ,x1x2=
,x1x2=![]() ,
,
又∠AOB为锐角,所以![]() ·
·![]() >0,即x1x2+y1y2>0,
>0,即x1x2+y1y2>0,
有x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4
=(1+k2)·![]() +2k·
+2k·![]() +4>0,解得k2<4,
+4>0,解得k2<4,
所以![]() <k2<4,即k∈
<k2<4,即k∈![]() .
.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
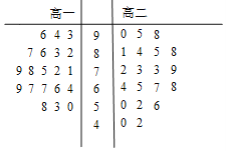
名牌学校分层周周测系列答案【题目】某学校为了解学生的体质健康状况,对高一、高二两个年级的学生进行了体质测试.现从两个年级学生中各随机选取20人,将他们的测试数据,用茎叶图表示如图:《国家学生体质健康标准》的等级标准如表.规定:测试数据≥60,体质健康为合格.
等级 | 优秀 | 良好 | 及格 | 不及格 |
测试数据 |
|
|
|
|
(Ⅰ)从该校高二年级学生中随机选取一名学生,试估计这名学生体质健康合格的概率;
(Ⅱ)从两个年级等级为优秀的样本中各随机选取一名学生,求选取的两名学生的测试数据平均数大于95的概率;
(Ⅲ)设该校高一学生测试数据的平均数和方差分别为![]() ,高二学生测试数据的平均数和方差分别为
,高二学生测试数据的平均数和方差分别为![]() ,试估计
,试估计![]() 、
、![]() 的大小.(只需写出结论)
的大小.(只需写出结论)