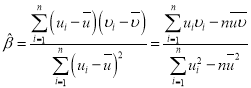题目内容
【题目】在平面直角坐标系![]() 中,抛物线C关于
中,抛物线C关于![]() 轴对称,顶点为坐标原点,且经过点
轴对称,顶点为坐标原点,且经过点![]() .
.
(1)求抛物线C的标准方程;
(2) 过点![]() 的直线交抛物线于M、N两点.是否存在定直线
的直线交抛物线于M、N两点.是否存在定直线![]() ,使得l上任意点P与点M,Q,N所成直线的斜率
,使得l上任意点P与点M,Q,N所成直线的斜率![]() ,
,![]() ,
,![]() 成等差数列.若存在,求出直线l的方程;若不存在,说明理由.
成等差数列.若存在,求出直线l的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)存在定直线,
;(2)存在定直线,![]() .
.
【解析】
(1)设抛物线为![]() ,代入点的坐标可得;
,代入点的坐标可得;
(2))假设存在直线![]() 使得直线上的任意点
使得直线上的任意点![]() 有
有![]() 成等差数列,设MN:
成等差数列,设MN:![]() 交抛物线于
交抛物线于![]() 、
、![]() ,代入抛物线方程应用韦达定理得
,代入抛物线方程应用韦达定理得![]() ,计算
,计算![]() ,
,![]() ,
,![]() ,并计算
,并计算![]() ,代入
,代入![]() 并化简,由
并化简,由![]() 为恒成立的,可求得
为恒成立的,可求得![]() .
.
(1)由条件设抛物线为![]() ,而点
,而点![]() 在抛物线上,
在抛物线上,
从而有![]() ,故抛物线方程为
,故抛物线方程为![]()
(2)假设存在直线![]() 使得直线上的任意点
使得直线上的任意点![]() 有
有![]() 成等差数列,
成等差数列,
由条件知直线MN的斜率不等于0,
设MN:![]() 交抛物线于
交抛物线于![]() 、
、![]() ,
,
由![]() 可得:
可得:![]()
从而有![]()
![]() ,
,![]() ,
,![]()
![]()
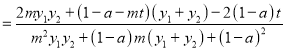
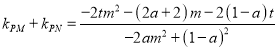
若![]() 成等差数列,则
成等差数列,则![]()
即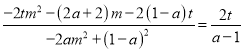
化简有![]()
从而有![]() ,即
,即![]()
故存在定直线![]() ,
,
使得l上任意点P与点M,Q,N所成直线斜率成等差数列

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
【题目】十八届五中全会首次提出了绿色发展理念,将绿色发展作为“十三五”乃至更长时期经济社会发展的一个重要理念.某地区践行“绿水青山就是金山银山”的绿色发展理念,2015年初至2019年初,该地区绿化面积y(单位:平方公里)的数据如下表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
绿化面积y | 2.8 | 3.5 | 4.3 | 4.7 | 5.2 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)利用(1)中的回归方程,预测该地区2025年初的绿化面积.
(参考公式:线性回归方程:![]() ,
,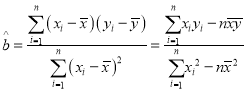 ,
,![]() 为数据平均数)
为数据平均数)